torch-optimizer
A collection of optimizers for Pytorch.
Simple example
import torch_optimizer as optim
# model = ...
optimizer = optim.DiffGrad(model.parameters(), lr=0.001)
optimizer.step()
Installation
Installation process is simple, just:
$ pip install torch_optimizer
Visualisations
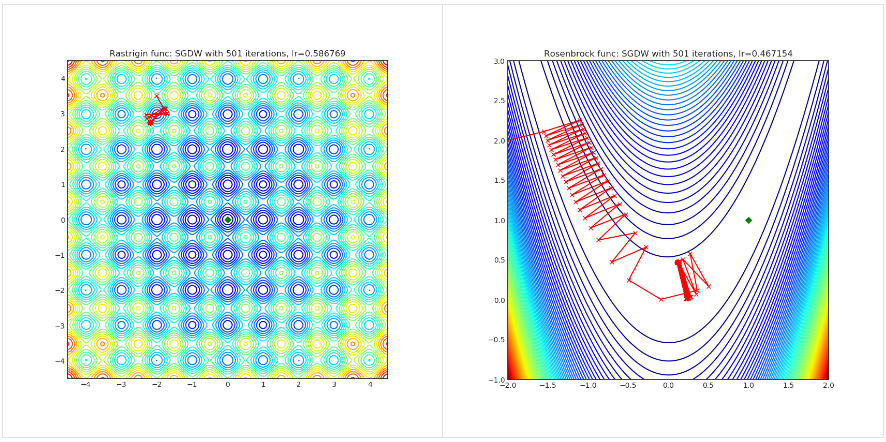
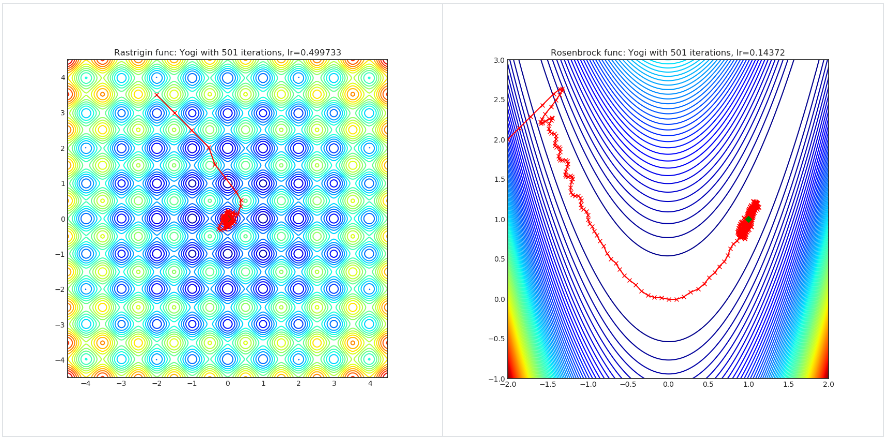
Visualisations help us to see how different algorithms deals with simple situations like: saddle points, local minima, valleys etc, and may provide interesting insights into inner workings of algorithm. Rosenbrock and Rastrigin benchmark functions was selected, because:
- Rosenbrock (also known as banana function), is non-convex function that has one global minima (1.0. 1.0). The global minimum is inside a long, narrow, parabolic shaped flat valley. To find the valley is trivial. To converge to the global minima, however, is difficult. Optimization algorithms might pay a lot of attention to one coordinate, and have problems to follow valley which is relatively flat.
-
Rastrigin function is a non-convex and has one global minima in (0.0, 0.0). Finding the minimum of this function is a fairly difficult problem due to its large search space and its large number of local minima.
Each optimizer performs 501 optimization steps. Learning rate is best one found by hyper parameter search algorithm, rest of tuning parameters are default. It is very easy to extend script and tune other optimizer parameters.
python examples/viz_optimizers.py
AccSGD
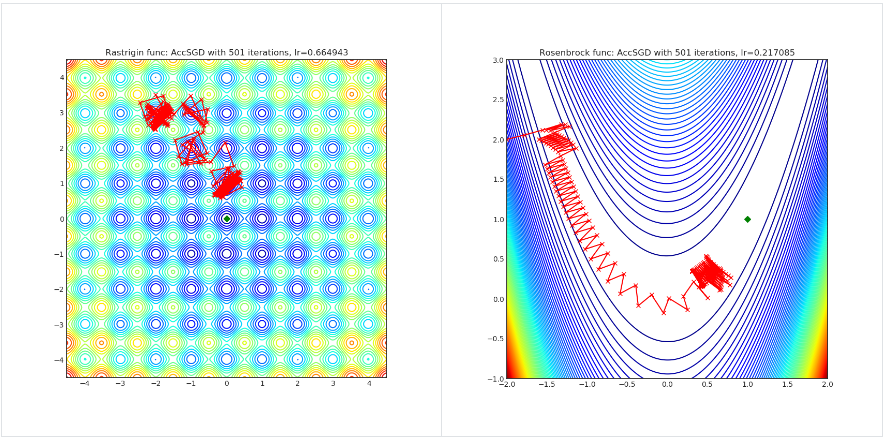
import torch_optimizer as optim
# model = ...
optimizer = optim.AccSGD(
model.parameters(),
lr=1e-3,
kappa=1000.0,
xi=10.0,
small_const=0.7,
weight_decay=0
)
optimizer.step()
Paper: On the insufficiency of existing momentum schemes for Stochastic Optimization (2019) [https://arxiv.org/abs/1803.05591]
Reference Code: https://github.com/rahulkidambi/AccSGD
AdaBound
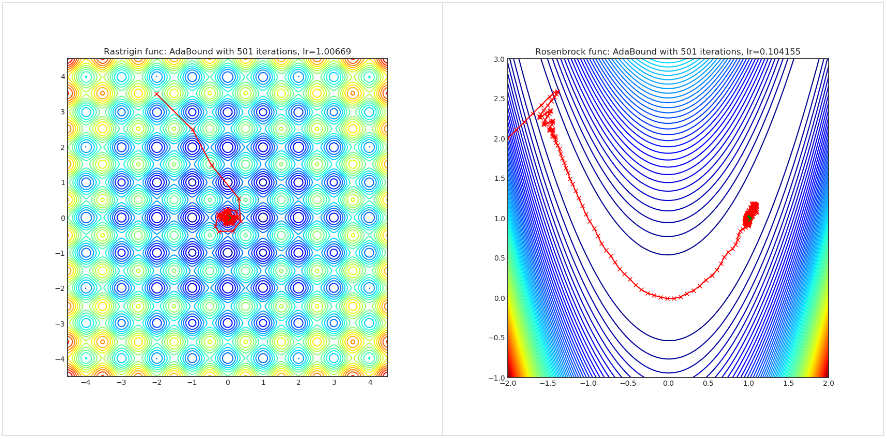
import torch_optimizer as optim
# model = ...
optimizer = optim.AdaBound(
m.parameters(),
lr= 1e-3,
betas= (0.9, 0.999),
final_lr = 0.1,
gamma=1e-3,
eps= 1e-8,
weight_decay=0,
amsbound=False,
)
optimizer.step()
Paper: Adaptive Gradient Methods with Dynamic Bound of Learning Rate (2019) [https://arxiv.org/abs/1902.09843]
Reference Code: https://github.com/Luolc/AdaBound
AdaMod
AdaMod method restricts the adaptive learning rates with adaptive and momental upper bounds. The dynamic learning rate bounds are based on the exponential moving averages of the adaptive learning rates themselves, which smooth out unexpected large learning rates and stabilize the training of deep neural networks.
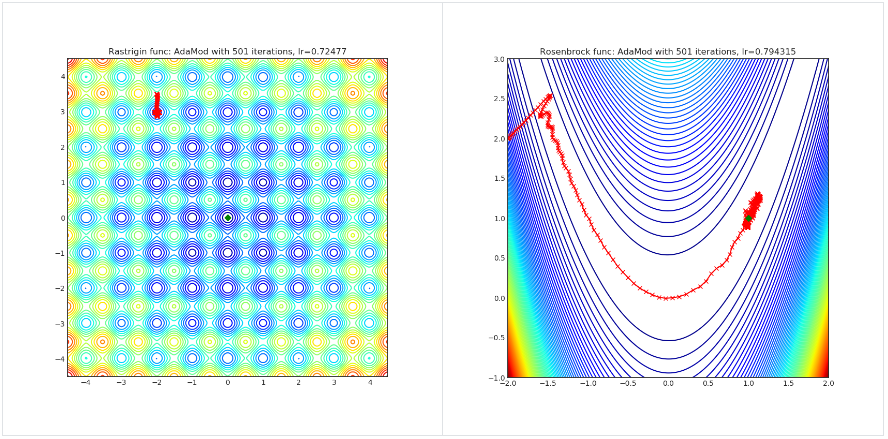
import torch_optimizer as optim
# model = ...
optimizer = optim.AdaMod(
m.parameters(),
lr= 1e-3,
betas=(0.9, 0.999),
beta3=0.999,
eps=1e-8,
weight_decay=0,
)
optimizer.step()
Paper: An Adaptive and Momental Bound Method for Stochastic Learning. (2019) [https://arxiv.org/abs/1910.12249]
Reference Code: https://github.com/lancopku/AdaMod
DiffGrad
Optimizer based on the difference between the present and the immediate past gradient, the step size is adjusted for each parameter in such a way that it should have a larger step size for faster gradient changing parameters and a lower step size for lower gradient changing parameters.
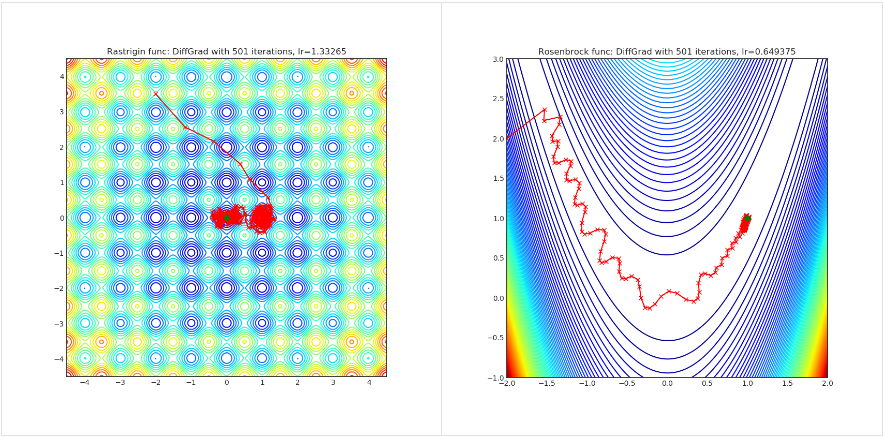
import torch_optimizer as optim
# model = ...
optimizer = optim.DiffGrad(
m.parameters(),
lr= 1e-3,
betas=(0.9, 0.999),
eps=1e-8,
weight_decay=0,
)
optimizer.step()
Paper: diffGrad: An Optimization Method for Convolutional Neural Networks. (2019) [https://arxiv.org/abs/1909.11015]
Reference Code: https://github.com/shivram1987/diffGrad
Lamb
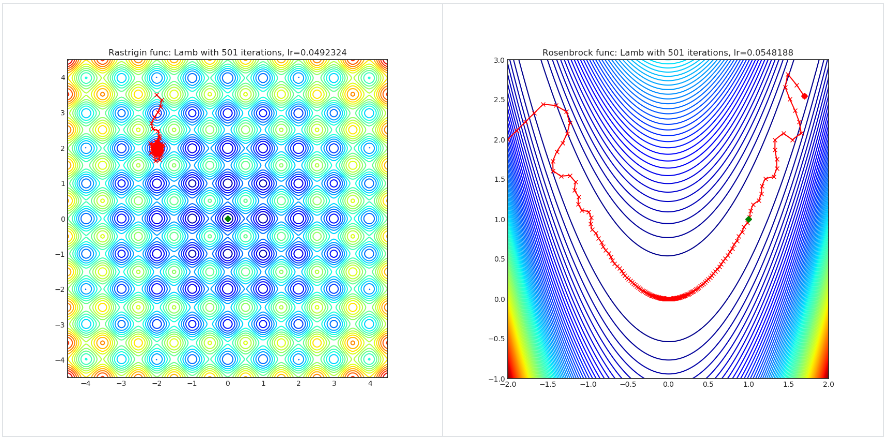
import torch_optimizer as optim
# model = ...
optimizer = optim.Lamb(
m.parameters(),
lr= 1e-3,
betas=(0.9, 0.999),
eps=1e-8,
weight_decay=0,
)
optimizer.step()
Paper: Large Batch Optimization for Deep Learning: Training BERT in 76 minutes (2019) [https://arxiv.org/abs/1904.00962]
Reference Code: https://github.com/cybertronai/pytorch-lamb
NovoGrad
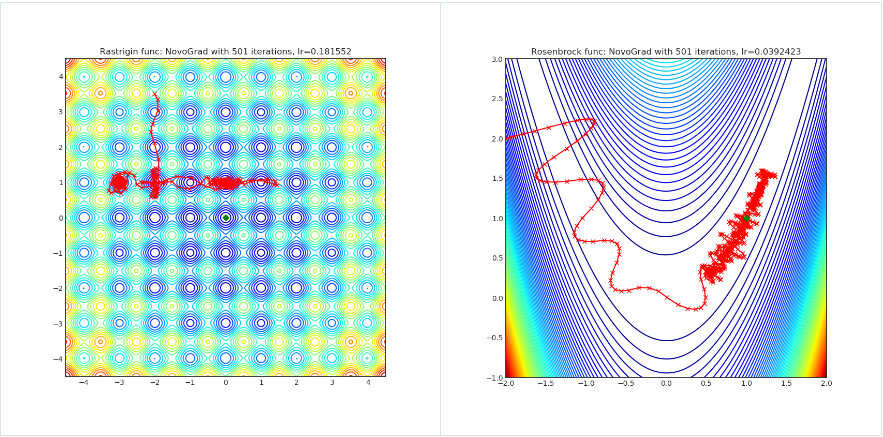
import torch_optimizer as optim
# model = ...
optimizer = optim.NovoGrad(
m.parameters(),
lr= 1e-3,
betas=(0.9, 0.999),
eps=1e-8,
weight_decay=0,
grad_averaging=False,
amsgrad=False,
)
optimizer.step()
Paper: Stochastic Gradient Methods with Layer-wise Adaptive Moments for Training of Deep Networks (2019) [https://arxiv.org/abs/1905.11286]
Reference Code: https://github.com/NVIDIA/DeepLearningExamples/
PID
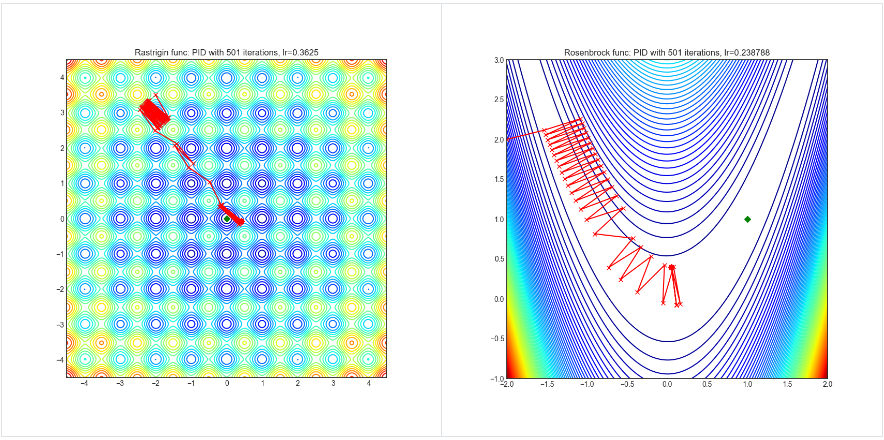
import torch_optimizer as optim
# model = ...
optimizer = optim.PID(
m.parameters(),
lr=1e-3,
momentum=0,
dampening=0,
weight_decay=1e-2,
integral=5.0,
derivative=10.0,
)
optimizer.step()
Paper: A PID Controller Approach for Stochastic Optimization of Deep Networks (2018) [http://www4.comp.polyu.edu.hk/~cslzhang/paper/CVPR18_PID.pdf]
Reference Code: https://github.com/tensorboy/PIDOptimizer
RAdam
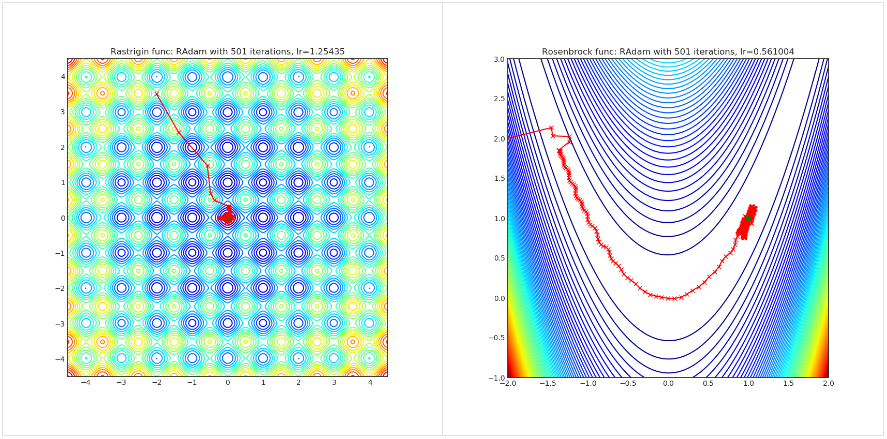
import torch_optimizer as optim
# model = ...
optimizer = optim.RAdam(
m.parameters(),
lr= 1e-3,
betas=(0.9, 0.999),
eps=1e-8,
weight_decay=0,
)
optimizer.step()
Paper: On the Variance of the Adaptive Learning Rate and Beyond (2019) [https://arxiv.org/abs/1908.03265]
Reference Code: https://github.com/LiyuanLucasLiu/RAdam
SGDW
import torch_optimizer as optim
# model = ...
optimizer = optim.SGDW(
m.parameters(),
lr= 1e-3,
momentum=0,
dampening=0,
weight_decay=1e-2,
nesterov=False,
)
optimizer.step()
Paper: SGDR: Stochastic Gradient Descent with Warm Restarts (2017) [https://arxiv.org/abs/1608.03983]
Reference Code: https://arxiv.org/abs/1608.03983
Yogi
Yogi is optimization algorithm based on ADAM with more fine grained effective learning rate control, and has similar theoretical guarantees on convergence as ADAM.
import torch_optimizer as optim
# model = ...
optimizer = optim.Yogi(
m.parameters(),
lr= 1e-2,
betas=(0.9, 0.999),
eps=1e-3,
initial_accumulator=1e-6,
weight_decay=0,
)
optimizer.step()
Paper: Adaptive Methods for Nonconvex Optimization (2018) [https://papers.nips.cc/paper/8186-adaptive-methods-for-nonconvex-optimization]
Reference Code: https://github.com/4rtemi5/Yogi-Optimizer_Keras



