potpourri3d
A Python library of various algorithms and utilities for 3D triangle meshes and point clouds. Managed by Nicholas Sharp, with new tools added lazily as needed. Currently, mainly bindings to C++ tools from geometry-central.
pip install potpourri3d
The blend includes:
- Mesh and point cloud reading/writing to a few file formats
- Use heat methods to compute distance, parallel transport, logarithmic maps, and more
Installation
Potpourri3d is on the pypi package index with precompiled binaries for most configuations. Get it like:
pip install potpourri3d
If none of the precompiled binaries match your system, pip will attempt to compile the library from scratch. This requires cmake and a workng C++ compiler toolchain.
Note: Some bound functions invoke sparse linear solvers internally. The precompiled binaries use Eigen's solvers; using Suitesparse's solvers instead may significantly improve performance & robustness. To get them, locally compile the package on a machine with Suitesparse installed using the command below (relevant docs).
python -m pip install potpourri3d --no-binary potpourri3d
Input / Output
Read/write meshes and point clouds from some common formats.
-
read_mesh(filename)Reads a mesh from file. Returns numpy matricesV, F, a Nx3 real numpy array of vertices and a Mx3 integer numpy array of 0-based face indices (or Mx4 for a quad mesh, etc).filenamethe path to read the file from. Currently supports the same file types as geometry-central. The file type is inferred automatically from the path extension.
-
write_mesh(V, F, filename)Write a mesh from file. Returns numpy matricesV, F, a Vx3 real array of vertices and a Fx3 integer array of 0-based face indices (or Fx4 for a quad mesh, etc).Va Nx3 real numpy array of verticesFa Mx3 integer numpy array of faces, with 0-based vertex indices (or Mx4 for a quad mesh, etc).filenamethe path to write the file to. Currently supports the same file types as geometry-central. The file type is inferred automatically from the path extension.
Mesh basic utilities
face_areas(V, F)computes a length-F real numpy array of face areas for a triangular meshvertex_areas(V, F)computes a length-V real numpy array of vertex areas for a triangular mesh (equal to 1/3 the sum of the incident face areas)cotan_laplacian(V, F, denom_eps=0.)computes the cotan-Laplace matrix as a VxV real sparse csr scipy matrix. Optionally, setdenom_epsto a small value like1e-6to get some additional stability in the presence of degenerate faces.
Mesh Distance
Use the heat method for geodesic distance to compute geodesic distance on surfaces. Repeated solves are fast after initial setup. Uses intrinsic triangulations internally for increased robustness.
import potpourri3d as pp3d
# = Stateful solves (much faster if computing distance many times)
solver = pp3d.MeshHeatMethodDistanceSolver(V,F)
dist = solver.compute_distance(7)
dist = solver.compute_distance_multisource([1,2,3])
# = One-off versions
dist = pp3d.compute_distance(V,F,7)
dist = pp3d.compute_distance_multisource(V,F,[1,3,4])
MeshHeatMethodDistanceSolver(V, F, t_coef=1., use_robust=True)construct an instance of the solver class.Va Nx3 real numpy array of verticesFa Mx3 integer numpy array of faces, with 0-based vertex indices (triangle meshes only, but need not be manifold).t_coefset the time used for short-time heat flow. Generally don't change this. If necessary, larger values may make the solution more stable at the cost of smoothing it out.use_robustuse intrinsic triangulations for increased robustness. Generaly leave this enabled.
MeshHeatMethodDistanceSolver.compute_distance(v_ind)compute distance from a single vertex, given by zero-based index. Returns an array of distances.MeshHeatMethodDistanceSolver.compute_distance_multisource(v_ind_list)compute distance from the nearest of a collection of vertices, given by a list of zero-based indices. Returns an array of distances.compute_distance(V, F, v_ind)Similar to above, but one-off instead of stateful. Returns an array of distances.compute_distance_multisource(V, F, v_ind_list)Similar to above, but one-off instead of stateful. Returns an array of distances.
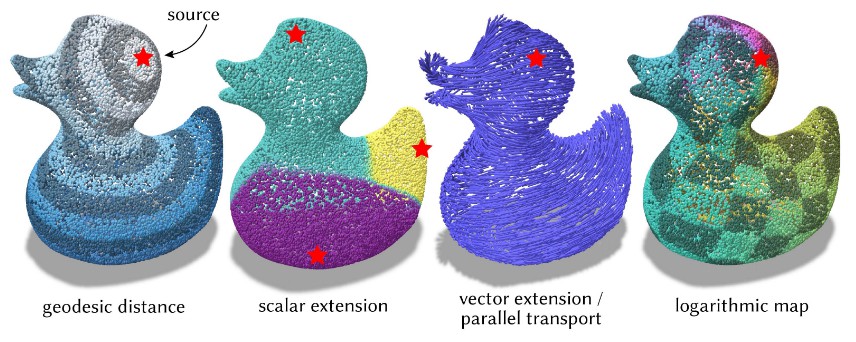
Mesh Vector Heat
Use the vector heat method to compute various interpolation & vector-based quantities on meshes. Repeated solves are fast after initial setup.
import potpourri3d as pp3d
# = Stateful solves
V, F = # a Nx3 numpy array of points and Mx3 array of triangle face indices
solver = pp3d.MeshVectorHeatSolver(V,F)
# Extend the value `0.` from vertex 12 and `1.` from vertex 17. Any vertex
# geodesically closer to 12. will take the value 0., and vice versa
# (plus some slight smoothing)
ext = solver.extend_scalar([12, 17], [0.,1.])
# Get the tangent frames which are used by the solver to define tangent data
# at each vertex
basisX, basisY, basisN = solver.get_tangent_frames()
# Parallel transport a vector along the surface
# (and map it to a vector in 3D)
sourceV = 22
ext = solver.transport_tangent_vector(sourceV, [6., 6.])
ext3D = ext[:,0,np.newaxis] * basisX + ext[:,1,np.newaxis] * basisY
# Compute the logarithmic map
logmap = solver.compute_log_map(sourceV)
MeshVectorHeatSolver(V, F, t_coef=1.)construct an instance of the solver class.Va Nx3 real numpy array of verticesFa Mx3 integer numpy array of faces, with 0-based vertex indices (triangle meshes only, should be manifold).t_coefset the time used for short-time heat flow. Generally don't change this. If necessary, larger values may make the solution more stable at the cost of smoothing it out.
MeshVectorHeatSolver.extend_scalar(v_inds, values)nearest-geodesic-neighbor interpolate values defined at vertices. Vertices will take the value from the closest source vertex (plus some slight smoothing)v_indsa list of source verticesvaluesa list of scalar values, one for each source vertex
MeshVectorHeatSolver.get_tangent_frames()get the coordinate frames used to define tangent data at each vertex. Returned as a tuple of basis-X, basis-Y, and normal axes, each as an Nx3 array. May be necessary for change-of-basis into or out of tangent vector convention.MeshVectorHeatSolver.transport_tangent_vector(v_ind, vector)parallel transports a single vector across a surfacev_indindex of the source vertexvectora 2D tangent vector to transport
MeshVectorHeatSolver.transport_tangent_vectors(v_inds, vectors)parallel transports a collection of vectors across a surface, such that each vertex takes the vector from its nearest-geodesic-neighbor.v_indsa list of source verticesvectorsa list of 2D tangent vectors, one for each source vertex
MeshVectorHeatSolver.compute_log_map(v_ind)compute the logarithmic map centered at the given source vertexv_indindex of the source vertex
Mesh Geodesic Paths
Use edge flips to compute geodesic paths on surfaces. These methods are especially useful when you want the path itself, rather than the distance. These routines use an iterative strategy which is quite fast, but note that it is not guaranteed to generate the globally-shortest geodesic (they sometimes find some other very short geodesic instead).

import potpourri3d as pp3d
V, F = # your mesh
path_solver = pp3d.EdgeFlipGeodesicSolver(V,F) # shares precomputation for repeated solves
path_pts = path_solver.find_geodesic_path(v_start=14, v_end=22)
# path_pts is a Vx3 numpy array of points forming the path
EdgeFlipGeodesicSolver(V, F)construct an instance of the solver class.Va Nx3 real numpy array of verticesFa Mx3 integer numpy array of faces, with 0-based vertex indices (must form a manifold, oriented triangle mesh).
EdgeFlipGeodesicSolver.find_geodesic_path(v_start, v_end)compute a geodesic fromv_starttov_end. Output is anNx3numpy array of positions which define the path as a polyline along the surface.EdgeFlipGeodesicSolver.find_geodesic_path_poly(v_list)likefind_geodesic_path(), but takes as input a list of vertices[v_start, v_a, v_b, ..., v_end], which is shorted to find a path fromv_starttov_end. Useful for finding geodesics which are not shortest paths. The input vertices do not need to be connected; the routine internally constructs a piecwise-Dijkstra path between them. However, that path must not cross itself.EdgeFlipGeodesicSolver.find_geodesic_loop(v_list)likefind_geodesic_path_poly(), but connects the first to last point to find a closed geodesic loop.
Point Cloud Distance & Vector Heat
Use the heat method for geodesic distance and vector heat method to compute various interpolation & vector-based quantities on point clouds. Repeated solves are fast after initial setup.
import potpourri3d as pp3d
# = Stateful solves
P = # a Nx3 numpy array of points
solver = pp3d.PointCloudHeatSolver(P)
# Compute the geodesic distance to point 4
dists = solver.compute_distance(4)
# Extend the value `0.` from point 12 and `1.` from point 17. Any point
# geodesically closer to 12. will take the value 0., and vice versa
# (plus some slight smoothing)
ext = solver.extend_scalar([12, 17], [0.,1.])
# Get the tangent frames which are used by the solver to define tangent data
# at each point
basisX, basisY, basisN = solver.get_tangent_frames()
# Parallel transport a vector along the surface
# (and map it to a vector in 3D)
sourceP = 22
ext = solver.transport_tangent_vector(sourceP, [6., 6.])
ext3D = ext[:,0,np.newaxis] * basisX + ext[:,1,np.newaxis] * basisY
# Compute the logarithmic map
logmap = solver.compute_log_map(sourceP)
PointCloudHeatSolver(P, t_coef=1.)construct an instance of the solver class.Pa Nx3 real numpy array of pointst_coefset the time used for short-time heat flow. Generally don't change this. If necessary, larger values may make the solution more stable at the cost of smoothing it out.
PointCloudHeatSolver.extend_scalar(p_inds, values)nearest-geodesic-neighbor interpolate values defined at points. Points will take the value from the closest source point (plus some slight smoothing)v_indsa list of source pointsvaluesa list of scalar values, one for each source points
PointCloudHeatSolver.get_tangent_frames()get the coordinate frames used to define tangent data at each point. Returned as a tuple of basis-X, basis-Y, and normal axes, each as an Nx3 array. May be necessary for change-of-basis into or out of tangent vector convention.PointCloudHeatSolver.transport_tangent_vector(p_ind, vector)parallel transports a single vector across a surfacep_indindex of the source pointvectora 2D tangent vector to transport
PointCloudHeatSolver.transport_tangent_vectors(p_inds, vectors)parallel transports a collection of vectors across a surface, such that each vertex takes the vector from its nearest-geodesic-neighbor.p_indsa list of source pointsvectorsa list of 2D tangent vectors, one for each source point
PointCloudHeatSolver.compute_log_map(p_ind)compute the logarithmic map centered at the given source pointp_indindex of the source point





