PyRoss: Infectious disease models in Python
PyRoss is a numerical library for mathematical modelling of infectious disease in Python. Currently the library supports structured compartment models formulated as systems of differential equations.
The library was developed to model the outbreak of the novel coronavirus COVID-19 and to assess the age-structured impact of social distancing measures in India.
The library is named after Sir Ronald Ross, doctor, mathematician and poet. In 1898 he made "the great discovery" in his laboratory in Calcutta "that malaria is conveyed by the bite of a mosquito". He won the Nobel Prize in 1902 and laid the foundations of the mathematical modelling of infectious diseases.
Publications
- Age-structured impact of social distancing on the COVID-19 epidemic in India, Rajesh Singh and R. Adhikari, arXiv:2003.12055.
Our latest forecast using case data until 25-03-2020:
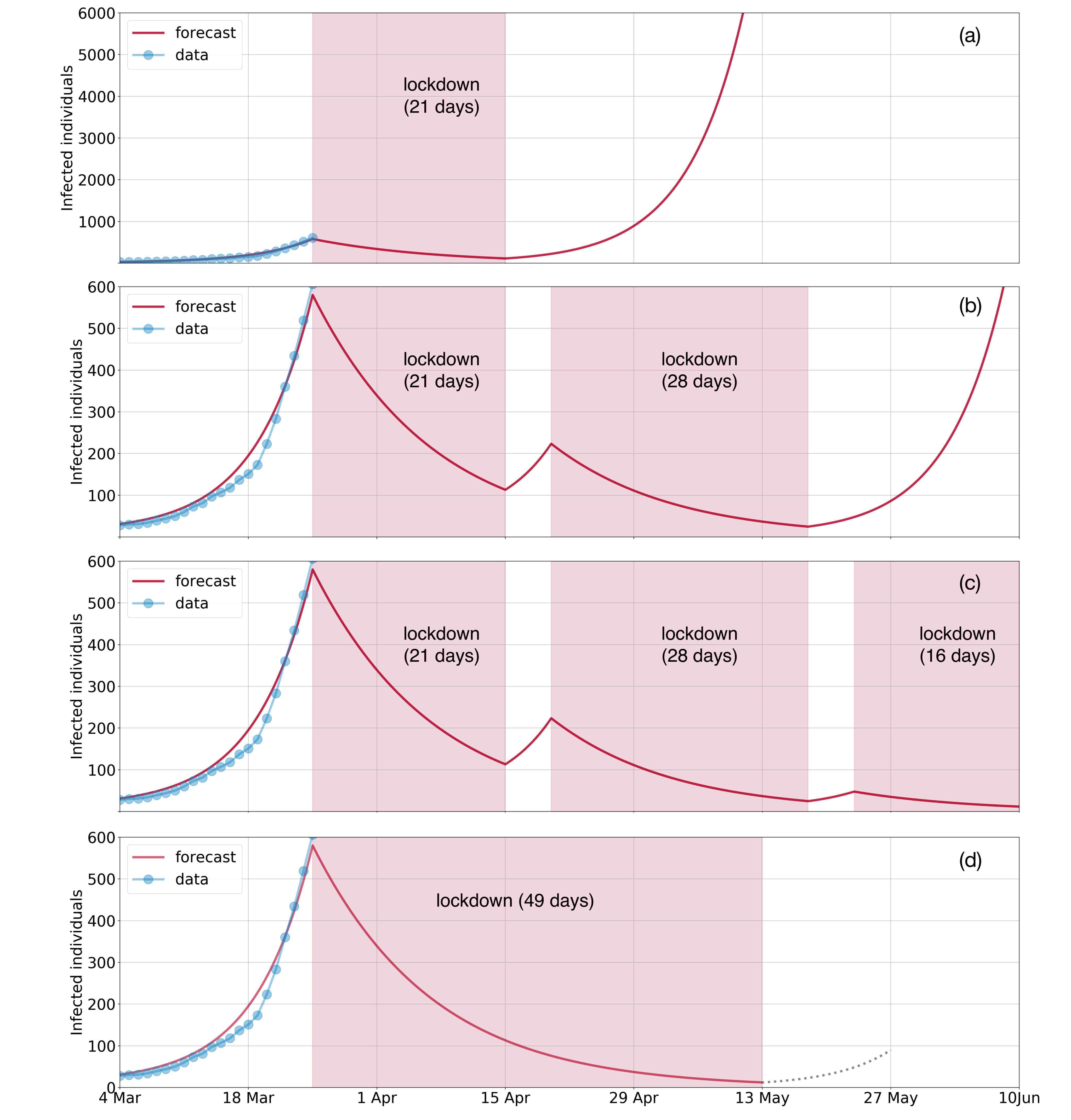
Installation
Clone (or download) the repository and use a terminal to install using
>> git clone https://github.com/rajeshrinet/pyross.git
>> cd pyross
>> python setup.py install
PyRoss requires the following software
- Python 2.6+ or Python 3.4+
- Cython 0.25.x+ | Matplotlib 2.0.x+ | NumPy 1.x+ | Pandas | SciPy 1.1.x+
Data sources
The age and social contact data that is needed to construct structured compartment models can be found at the following sources:
Age structure: Population Pyramid website.
Contact structure: Projecting social contact matrices in 152 countries using contact surveys and demographic data, Kiesha Prem, Alex R. Cook, Mark Jit, PLOS Computational Biology, (2017) DOI, Supporting Information Text and Supporting Information Data.
The list of COVID-19 cases is obtained from the Worldometer website.
Examples
#Ex1: M=1
import numpy as np
import pyross
M = 1 # the SIR model has no age structure
Ni = 1000*np.ones(M) # so there is only one age group
N = np.sum(Ni) # and the total population is the size of this age group
beta = 0.2 # infection rate
gamma = 0.1 # recovery rate
alpha = 0 # fraction of asymptomatic infectives
fsa = 1 # the self-isolation parameter
Ia0 = np.array([0]) # the SIR model has only one kind of infective
Is0 = np.array([1]) # we take these to be symptomatic
R0 = np.array([0]) # and assume there are no recovered individuals initially
S0 = N-(Ia0+Is0+R0) # so that the initial susceptibles are obtained from S + Ia + Is + R = N
# there is no contact structure
def contactMatrix(t):
return np.identity(M)
# duration of simulation and data file
Tf = 160; Nt=160; filename = 'this.mat'
# instantiate model
model = pyross.models.SIR(alpha, beta, gamma, fsa, M, Ni)
# simulate model
model.simulate(S0, Ia0, Is0, contactMatrix, Tf, Nt, filename)
-
See the examples folder for a list of worked out examples.
-
State-wise prediction of COVID-19 in India using PyRoss by Ashish Kumar and Mohit Chaukikar



