My notes on DS and Algo
My notes on Data structure and Algos in golang implementation and python
Arrays
Advantages of array
- Reading and writing is O(1)
Disadvantages of array
- Insertion and deletion is O(n)
- Arrays are not dynamic
- If you need to store an extra element, you would have to create a new array and copy all the elements over. O(n)
List Slicing in python
- [start:stop:step]
- Reverse a list
list[::-1]
LinkedList
- Linked lists are great for problems that require arbitrary insertion.
- Dynamic arrays allow inserting at arbitrary locations, but they require you to move all elements after your insertion point.
- Doubly LinkedLists don’t have this problem: you can insert or delete elements in a linked list in constant time, as long as you know where the element is.
- The downside is that they don’t allow constant time access: to find the ith element, you need to traverse i elements, whereas arrays can do this in constant time. .
- Use them where insertion speed is important, but not when you want to access elements based on their index.

Trees
Types of trees:
- Binary Search Tree (most interview questions are asking about binary search trees)
- for each node, its left child is less than the node, which is less than its right child.
- Balanced
- Balanced means the difference between the heights of the left and right subtrees is no more than 1.
- This ensures O(log n) time for both search and insert.
- Complete
- A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
- Full
- A full binary tree is a binary tree in which every node has either 0 or 2 children.
- Perfect
- Full & Complete
- Binary Heaps (Min/Max)
- Complete Binary Search Tree where each node is smaller than its childs.
- the root is the minimum
- Tries(Prefix Trees)
Binary Search Tree
Binary search trees are useful, because they allow you to find elements in O(log n) time, but unlike a sorted array, you can do insertions at an average of O(log n) time, as opposed to O(n) potentially.

Heap
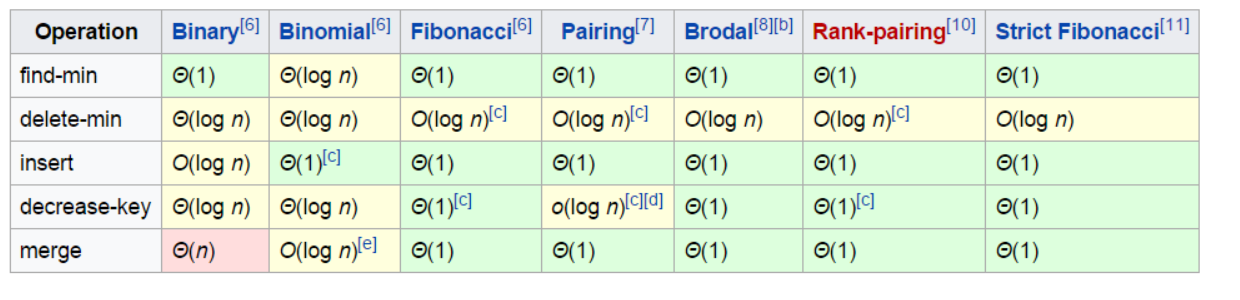
Priority Queue
Priority queue is an abstract data type (an interface definition) that defines three operations: is_empty, insert_with_priority, and pull_highest_priority_element. The definition says what those functions are expected to do, but it doesn't say how it is to be implemented.
A binary heap is one way to implement a priority queue. Its advantages are ease of implementation and that it is reasonably efficient.
Trie
- A trie is a kind of tree data structure that is used to store a dynamic set of strings.
- A trie is a tree where each node represents a prefix (or partial key).
- Booleans are used to indicate if a prefix is a complete key or not.
Advantages of using Trie:
It can tell us if a string is a prefix of any valid words and a tree can do it in O(K) time where K is the length of the string.
Many problems involving list of words can be solved using a trie. In situations when we search through the tree on related prefixes repeatedly (e.g looking up M, then MA,MAN,MANY) we might pass a reference to the current node in the tree
Key Functions:
insert: Inserts a new key into the trie.
1. For each character in the word, create a new node as a child of the current node if it does not already exist.
2. Mark the current node as complete if it is a prefix of the word.
search: Searches for a key in the trie.
Time Complexity:
insert: O(lg n)search: O(m) where m is the length of the key.- Tradoff?
Use case:
- many problems involving lists of words leverage trie as optimisation
- Storing a dictionary of words for quick lockup
- autocomplete
Graphs
Representing Graphs :
Every Vertex stores a list of adjacent vertices.
Each index of a list could be used to represent the vertex and the elements represent adjacent vertices.
Representing graphs as 2 dimensional matrix.
- Edge is represented by the value of i,j in matrix.
- To add a vertex, add a row and column
If the graph is weighted, the value of each matrix would be the weights instead of 1s and 0s.
If the graph is undirected, it means that there is symmetry about the diagonal of the matrix, because the edges are bi-directional.
Comparing Adjacency Matrix and List
Matrix requries more space. n^2
Adjancy matrix is faster for Edge lookup O(1) vs O(V)
Time Complexity
Tree/Graph Traversal Algorithms
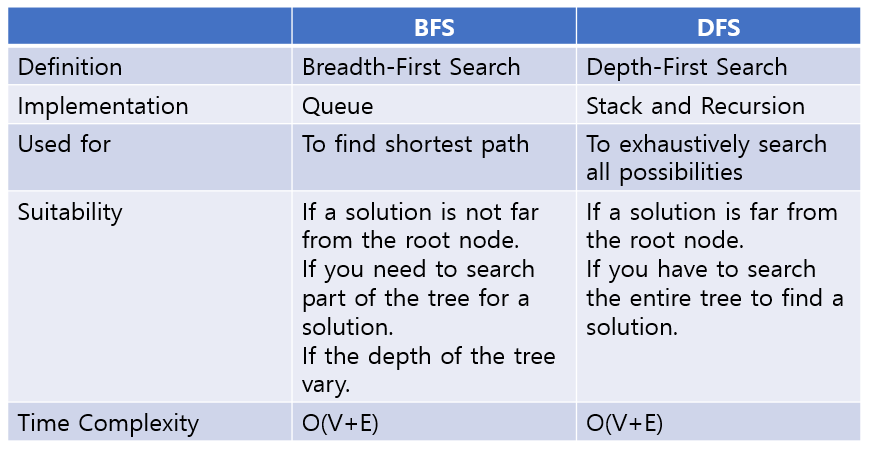
Breadth-first search is guaranteed to find a shortest possible path between two vertices in a graph. Depth-first search is not (and usually does not).
DFS is preferred if we want to visit every node in the graph.
DFS : Stack ; BFS : Queue
Binary Tree Traversal
In order
1. Visit Left Node
1. Current Node
1. Right Node
Pre Order
1. Visit Current Node
1. Visit Left Node
1. Visit Right Node
Post Order
1. Visit Left
1. Right
1. Current
Depth-First Traversal
- DFS is a recursive algorithm that visits every node in a graph, starting from the source node and proceeding along the edges of the graph.
- DFS implements the order traversal just that it has 'visited' mark, so that it does not repeat the visiting.
Breadth-First Traversal
- BFS is a iterative algorithm that uses a queue to store the nodes that need to be visited.
Algorithm:
1. Enqueue the source node
2. while the queue is not empty, dequeue a node
3. Visit the node if not visited
4. Enqueue the children of the node
DFS VS BFS
Topological Sort
Topological Sort is a linear ordering of vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering.

Degree of a vertex is the number of edges connected to it.
| In degree : | Out degree : |
|---|---|
| In degree is the number of edges coming into a vertex. In degree is 0 if the vertex is a leaf node. | Out degree is the number of edges going out of a vertex. |
Applications
- Task Scheduling
- Build Systems
- Course Scheduling
Algorithm:
1. Create a set of all vertices with no incoming edges
2. While there are vertices in the set
1. Pick a vertex u
2. Remove u from the set
3. For each vertex v such that there is an edge from u to v
1. Remove edge uv from graph
2. Add v to the set
Algorithms
Others

Stable : Maintains the relative order of elements with the same key.
Online : Algorithm can operate without seeing the entire list of elements. O(1)
In place : Uses additional space to store the result.



