Connex
Connex is a small JAX library built on Equinox inspired by two features of biological neural networks:
- Complex Connectivity: Turn any directed acyclic graph (DAG) into a trainable neural network.
- Plasticity: Add and remove both connections and neurons at the individual level.
Installation
pip install connex
Requires Python 3.7+, JAX 0.3.4+, and Equinox 0.5.2+.
Documentation
Available here.
Usage
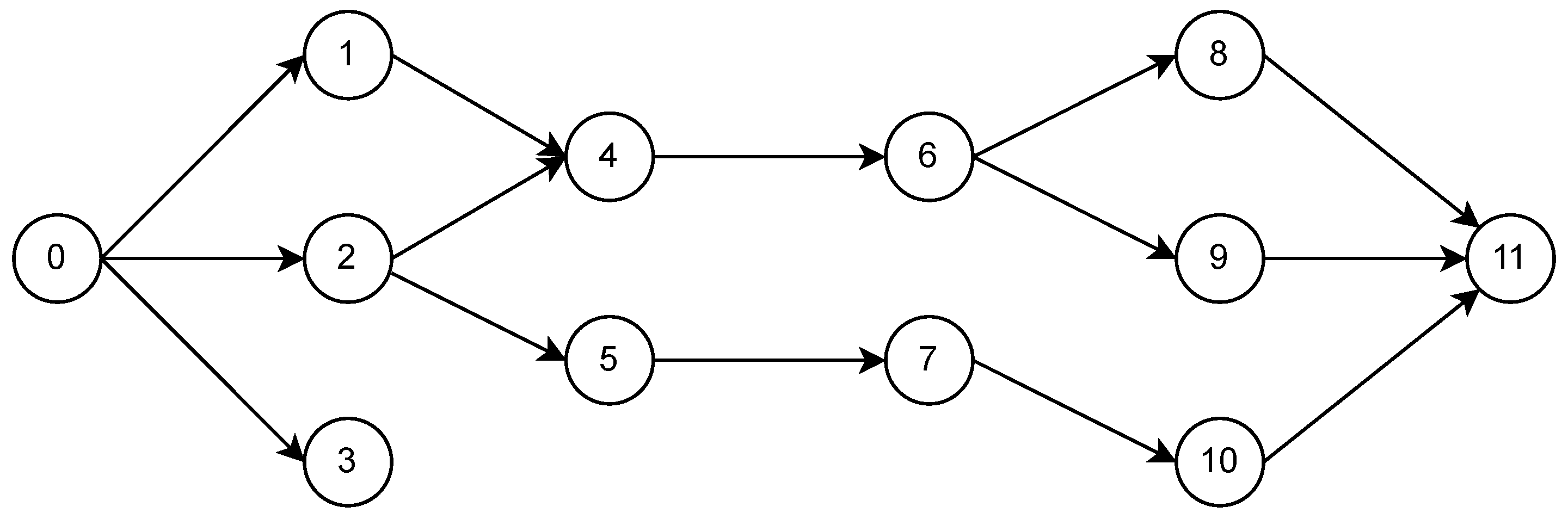
Suppose we would like to create a trainable neural network from the following DAG
with input neuron 0 and output neurons 3 and 11 (in that order), with a jax.nn.relu activation function for the hidden neurons:
import connex as cnx
import jax.nn as jnn
# Specify number of neurons
num_neurons = 12
# Build the adjacency dict
adjacency_dict = {
0: [1, 2, 3],
1: [4],
2: [4, 5],
4: [6],
5: [7],
6: [8, 9],
7: [10],
8: [11],
9: [11],
10: [11]
}
# Specify the input and output neurons
input_neurons = [0]
output_neurons = [3, 11]
# Create the network
network = cnx.NeuralNetwork(
num_neurons,
adjacency_dict,
input_neurons,
output_neurons,
jnn.relu
)
That’s it! A connex.NeuralNetwork is a subclass of equinox.Module, so it can be trained in the same fashion:
import equinox as eqx
import jax
import jax.numpy as jnp
import optax
# Initialize the optimizer
optim = optax.adam(1e-3)
opt_state = optim.init(eqx.filter(network, eqx.is_array))
# Define the loss function
def loss_fn(model, x, y):
preds = jax.vmap(model)(x)
return jnp.mean((preds - y) ** 2)
# Define a single training step
@eqx.filter_jit
def step(model, optim, opt_state, X_batch, y_batch):
loss, grads = eqx.filter_value_and_grad(loss_fn)(model, X_batch, y_batch)
updates, opt_state = optim.update(grads, opt_state, model)
model = eqx.apply_updates(model, updates)
return model, opt_state, loss
# Toy data
X = jnp.expand_dims(jnp.linspace(0, 2 * jnp.pi, 250), 1)
y = jnp.hstack((jnp.cos(X), jnp.sin(X)))
# Training loop
n_epochs = 1000
for _ in range(n_epochs):
network, opt_state, loss = step(network, optim, opt_state, X, y)
Now suppose we wish to add connections 1 → 6 and 2 → 11, and remove neuron 9:
# Add connections
network = cnx.add_connections(network, [(1, 6), (2, 11)])
# Remove neuron
network, _ = cnx.remove_neurons(network, [9])
That’s all there is to it. The parameters have been retained for neurons in the original network that have not been removed. connex.remove_neurons also returns auxiliary information about neuron ids, since removal of neurons re-numbers the remaining ones.
For more information about manipulating connectivity structure and the NeuralNetwork base class, please see the API section of the documentation. For examples of subclassing NeuralNetwork, please see connex.nn.
Feedback is greatly appeciated!