pynm
NeuroMorphic Predictive Model with Spiking Neural Networks (SNN) in Python using Pytorch.
pynm is an open source, low-code library in python to build neuromorphic predictive models (Classification & Regression problems) using [Spiking Neural Networks (SNNs)] (https://en.wikipedia.org/wiki/Spiking_neural_network) at ease. It allows you to go from preparing your data to deploying your spiking model within minutes. SNNs are neural networks that mimics the biological brain. In the case of SNNs, the neurons accumulate the input activation until a threshold is reached, and when this threshold is reached, the neuron empties itself from it's activation and fire. Once empty, it should indeed take some refractory period until it fires again, as it happen in the brain.
pynm is simple, easy to use and low-code. It enables users to perform end-to-end Proof-Of-Concept (POC) experiments quickly and efficiently.
Who should use pynm?
PYNM is an open source library ideal for:-
- Citizen Data Scientists who prefer a low code solution.
- Experienced Data Scientists who want to increase model accuracy and improve productivity.
- Data Science Professionals and Consultants involved in building proof-of-concept (poc) projects.
- Researchers for quick poc testing.
- Students and Teachers.
- ML Enthusiasts.
Neuromorphic Design with SNN
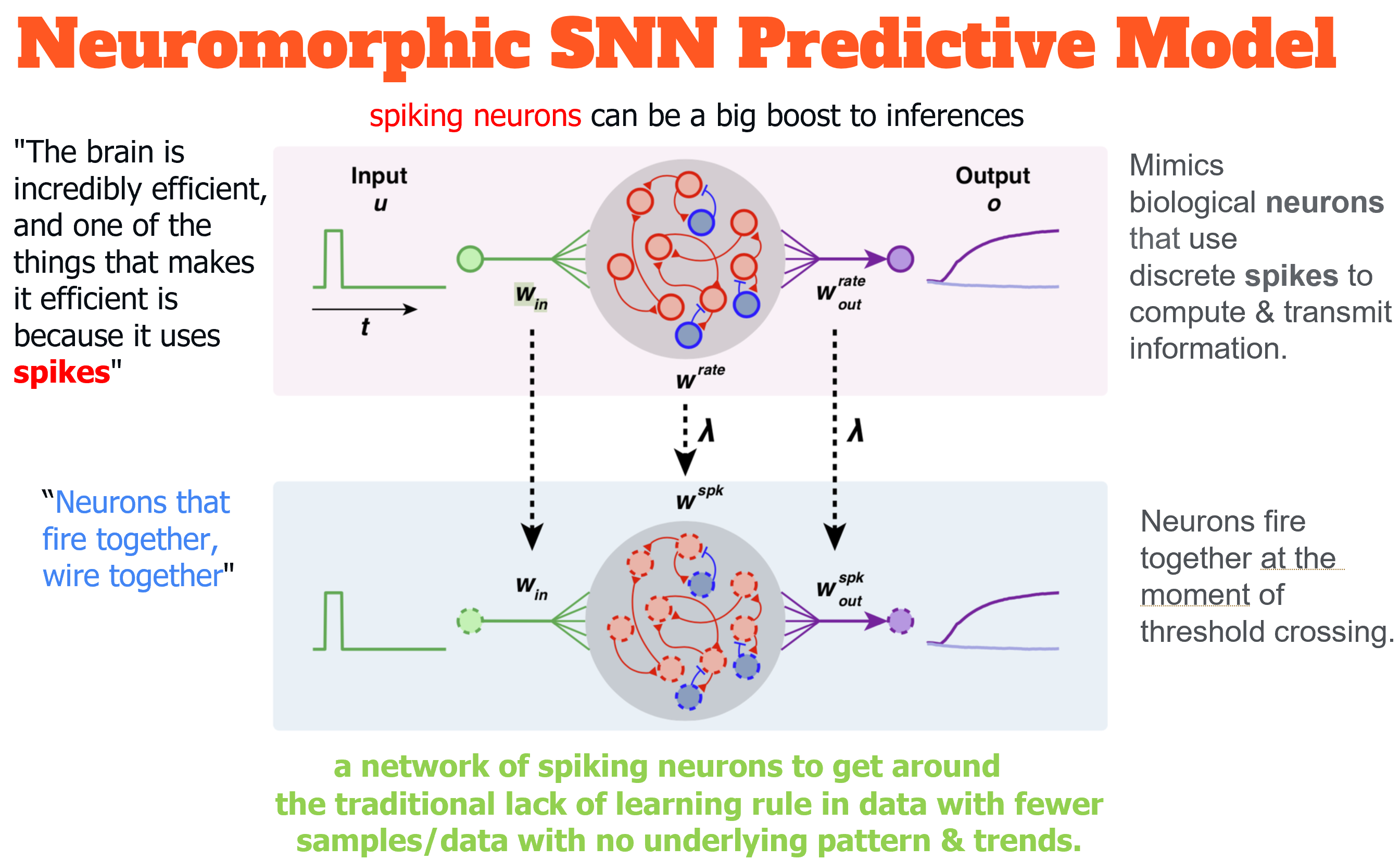
Neuromorphic design finds new life in machine learning. Neuromorphic architecture has had little practical success in building machines that can tackle standard tests such as logistic regression or image recognition. But lately it has been combined with the best of machine learning, and the networks of spiking neurons, bringing new hope for neuromorphic breakthroughs. Neuromorphic computing is an umbrella term given to a variety of efforts to build computation that resembles some aspect of the way the brain is formed. The brain is incredibly efficient, and one of the things that makes it efficient is because it uses spikes. If we can get a model of a spiking neurons as part of deep nets, it can be a big boost to inference, the task of making predictions, even on the energy-constrained edge computing devices such as mobile phones.
SNN vs ANN
In SNNs, there is a time axis and the neural network sees data througout time, and activation functions are spikes that are raised past a certain pre-activation threshold. Pre-activation values constantly fades if neurons aren't excited enough. Think of it like a time-distributed ReLU with spikes or no spikes at certain time steps.
Spiking Neural Networks (SNNs) are neural networks that are closer to what happens in the brain compared to what people usually code when doing Machine Learning and Deep Learning. In the case of SNNs, the neurons accumulate the input activation until a threshold is reached, and when this threshold is reached, the neuron empties itself from it's activation and fire. Once empty, it should indeed take some [refractory period](https://en.wikipedia.org/wiki/Refractory_period_(physiology) until it fires again, as it happen in the brain.
This implies adding a time axis to Artificial Neural Networks (ANNs), where signal is accumulated throughout time in a pre-activation phase, then once a threshold is reached, signal is raised to the neurons above as a firing activation. At every moment, such as when the threshold isn't reached yet, the signal's pre-activation value fades.
For more detail information about SNNs you are recommended to watch [this interesting SNN animation](https://www.youtube.com/embed/3JQ3hYko51Y?start=120) which will quickly get you a feel of what it is (especially notice how neurons gets activated only gradually over time like a storm that fire together rather than statically from their inputs).
Why Neuromorphic Predictive Model?
The concept is as given in the figure.
How does it work?
The neuron's firing method is through the following steps, where the argument x is an input:
Before anything, we need an initialize (or to empty) the state for each neuron upon starting predictions.
self.prev_inner = torch.zeros([batch_size, self.n_hidden]).to(self.device)
self.prev_outer = torch.zeros([batch_size, self.n_hidden]).to(self.device)
Then, a weight matrix multiplies the input x, which is the input dataset. It is to be noted that x was modified to be flickering randomly through time (depending on the intensity of the original input x multiplied by a random uniform noise mask), or else x is already the output of a lower deep spiking layer:
input_excitation = self.fully_connected(x)
We then add the result to a decayed version of the information inside the neuron that we already had at the previous time step / time tick (Δt time elapsed). The decay_multiplier serves the purpose of slowly fading the inner activation such that we don't accumulate stimulis for too long to be able to have the neurons to rest. The decay_multiplier could have a value of 0.9 for example. Decay as such is also called exponential decay and yields an effect of [Exponential moving average](https://en.wikipedia.org/wiki/Moving_average#Exponential_moving_average) over time on the most recent values seen, which also affects the gradients upon backpropagating. So, by repeatedly multplying by 0.9 the inner activation through time, it decays and neurons unexcite themselves before firing. In this sense, it's now really true that "neurons that fire together wire together": when a pre-synaptic input is received closer to the moment of giving an output, that recentmost value will not have had the time to be decayed/faded. This way, the gradient of recent neurons that participated in exciting the current neuron that fired will be strong. Learning will be able to take place by gradient descent according to the decay's weighting's. So, in the opposite case, a stimuli that happened too long ago will suffer from vanishing gradients since it has been exponentially decayed down. So, it won't be useful in the learning process of backprop, which is what we want and respects the "neurons that fire together, wire together" idiom of Hebbian learning.
inner_excitation = input_excitation + self.prev_inner * self.decay_multiplier
Now, we compute the activation of the neurons to find their output value. We have a threshold to reach before having the neuron activating. The ReLU function might not be the most appropriate here, but just for a working prototype ReLU was used:
outer_excitation = F.relu(inner_excitation - self.threshold)
Now, the magic happens. If the neuron fires, the activation of the neuron is subtracted to its inner state to reset each neuron. First, this has the effect of resetting them to a resting position such that they won't be firing constantly upon being activated once. Second, resetting them as such will clip the gradient through time to isolate each firing events from each other. SNNs as such are truly inspired from the brain, as the natural neurons also have a refractory period: neurons, once they fire, will need to wait a bit before firing again even if fully excited by lower neurons they have as inputs. So here, I even subtracted a second penalty named penalty_threshold after each resetting threshold. Disclaimer:- I wasn't sure whether the negative part in the biological refractory period was on the outputs of the neurons or inside the neurons (e.g.: axon v.s. body?), so here I've simply put it inside. Let's see how I subtract this just when the neuron fires to have it to have a refractory period:
do_penalize_gate = (outer_excitation > 0).float()
inner_excitation = inner_excitation - (self.penalty_threshold + outer_excitation) * do_penalize_gate
Finally, I return the previous output, simulating a small firing delay, which may not be useful in all the case, but which may be interesting to have if the SNN that is designed was ever to have Recurrent connections which would require time offsets in the connections from top layers near the outputs back into bottom layers near the input:
delayed_return_state = self.prev_inner
delayed_return_output = self.prev_outer
self.prev_inner = inner_excitation
self.prev_outer = outer_excitation
return delayed_return_state, delayed_return_output
Past that, to do the classification, the values of the classification output spiking neurons are averaged over the time axis so as to have one number per class to plug into the softmax cross entropy loss for classification as we know it and we backpropagate. This means the present SNN PyTorch class is reusable within any other feedforward neural network, as it repeats intputs over time with random noisy masks, and averages outputs over time.
Basically, the neurons' activation must decay through time, and fire only when getting past a certain threshold.
Requirements
- Python 3.6.x
- torch[>=1.4.0]
- NumPy[>=1.9.0]
- SciPy[>=0.14.0]
- Scikit-learn[>=0.16]
- Pandas[>=0.23.0]
- Xgboost[>=1.4.1]
- Matplotlib
- Seaborn[0.9.0]
- Plot-metric
- regressioncomparemetricplot
- tqdm
Quickly Setup package with automation scripts
sudo bash setup.sh
Installation
Using pip:
pip install pynm
$ git clone https://github.com/ajayarunachalam/pynm
$ cd pynm
$ python setup.py install
Using notebook:
!pip install pynm
Getting started
- DEMO:
Example MultiClass Classification: IRIS dataset
__author__ = 'Ajay Arunachalam'
__version__ = '0.0.1'
__date__ = '19.7.2021'
from spiking_multiclass_classifier import *
import torch
import torch.nn.functional as F
import torch.nn as nn
from torch.autograd import Variable
from torch.utils.data import Dataset, DataLoader
import torch.optim as optim
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, precision_score, recall_score
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from xgboost import XGBRegressor
from tqdm.notebook import tqdm
from sklearn.datasets import load_iris
from sklearn.metrics import roc_curve, auc
from sklearn.metrics import confusion_matrix
from cf_matrix import make_confusion_matrix
from plot_metric.functions import MultiClassClassification
import seaborn as sns
from random import *
get_ipython().run_line_magic('matplotlib', 'inline')
def run_classifier():
torch.multiprocessing.freeze_support()
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(device)
# load iris dataset
iris_df = pd.read_csv('../data/iris_data.csv')
print(iris_df.shape)
print(iris_df.head())
# transforming target/class to numeric
#iris_df.loc[iris_df.species=='Iris-setosa','species'] = 0
#iris_df.loc[iris_df.species=='Iris-versicolor','species'] = 1
#iris_df.loc[iris_df.species=='Iris-virginica','species'] = 2
#checking class distribution
iris_df['target'].value_counts().plot.bar(legend='Class Distribution')
# final dataset
X = iris_df.iloc[:,0:4]
y = iris_df.iloc[:,4]
#print(y)
# Scale data to have mean '0' and variance '1'
# which is importance for convergence of the neural network
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Split the data set into training and testing
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y.values.astype(float), test_size=0.2, random_state=2)
#####################
spiking_model = SpikingNeuralNetwork(device, X_train.shape[1], num_class=3, n_time_steps=64, begin_eval=0)
#####################
optimizer = torch.optim.Adam(spiking_model.parameters(), lr=0.001)
#optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
loss_fn = nn.CrossEntropyLoss()
print(spiking_model)
# Train the model
EPOCHS = 100
X_train = Variable(torch.from_numpy(X_train)).float()
y_train = Variable(torch.from_numpy(y_train)).long()
X_test = Variable(torch.from_numpy(X_test)).float()
y_test = Variable(torch.from_numpy(y_test)).long()
loss_list = np.zeros((EPOCHS,))
accuracy_list = np.zeros((EPOCHS,))
for epoch in tqdm(range(EPOCHS)):
y_pred = spiking_model(X_train) #model
#print(y_pred)
loss = loss_fn(y_pred, y_train)
loss_list[epoch] = loss.item()
# Zero gradients
optimizer.zero_grad()
loss.backward()
optimizer.step()
with torch.no_grad():
y_pred = spiking_model(X_test) #model
correct = (torch.argmax(y_pred, dim=1) == y_test).type(torch.FloatTensor)
accuracy_list[epoch] = correct.mean()
if epoch % 10 == 0:
print('number of epoch', epoch, 'loss', loss.item())
print('number of epoch', epoch, 'accuracy', correct[0])
# Plot Accuracy and Loss from Training
fig, (ax1, ax2) = plt.subplots(2, figsize=(12, 6), sharex=True)
ax1.plot(accuracy_list)
ax1.set_ylabel("validation accuracy")
ax2.plot(loss_list)
ax2.set_ylabel("validation loss")
ax2.set_xlabel("epochs");
# Show ROC Curve
plt.figure(figsize=(10, 10))
plt.plot([0, 1], [0, 1], 'k--')
# One hot encoding
enc = OneHotEncoder()
Y_onehot = enc.fit_transform(y_test[:, np.newaxis]).toarray()
with torch.no_grad():
y_pred = spiking_model(X_test).numpy() #model
#pred = torch.argmax(y_pred).type(torch.FloatTensor)
fpr, tpr, threshold = roc_curve(Y_onehot.ravel(), y_pred.ravel())
plt.plot(fpr, tpr, label='AUC = {:.3f}'.format(auc(fpr, tpr)))
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC curve')
plt.legend();
print(y_test)
print(np.argmax(y_pred, axis=1))
y_pred_ = np.argmax(y_pred, axis=1)
#Get the confusion matrix
cf_matrix = confusion_matrix(y_test, y_pred_)
print(cf_matrix)
make_confusion_matrix(cf_matrix, figsize=(8,6), cbar=False, title='IRIS CF Matrix')
# report
# Visualisation of plots
mc = MultiClassClassification(y_test, y_pred, labels=[0, 1, 2])
plt.figure(figsize=(13,4))
plt.subplot(131)
mc.plot_roc()
plt.subplot(132)
mc.plot_confusion_matrix()
plt.subplot(133)
mc.plot_confusion_matrix(normalize=True)
plt.savefig('../figures/images/plot_multi_classification.png')
plt.show()
mc.print_report()
if (__name__ == '__main__'):
run_classifier()
Example MultiClass Classification: MNIST dataset
import os
import matplotlib.pyplot as plt
import torchvision.datasets
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision.transforms as transforms
from torch.autograd import Variable
import numpy as np
import pandas as pd
def train(model, device, train_set_loader, optimizer, epoch, logging_interval=100):
model.train()
for batch_idx, (data, target) in enumerate(train_set_loader):
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % logging_interval == 0:
pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability
correct = pred.eq(target.view_as(pred)).float().mean().item()
print('Train Epoch: {} [{}/{} ({:.0f}%)] Loss: {:.6f} Accuracy: {:.2f}%'.format(
epoch, batch_idx * len(data), len(train_set_loader.dataset),
100. * batch_idx / len(train_set_loader), loss.item(),
100. * correct))
def train_many_epochs(model):
epoch = 1
optimizer = optim.SGD(model.parameters(), lr=0.1, momentum=0.5)
train(model, device, train_set_loader, optimizer, epoch, logging_interval=10)
test(model, device, test_set_loader)
epoch = 2
optimizer = optim.SGD(model.parameters(), lr=0.05, momentum=0.5)
train(model, device, train_set_loader, optimizer, epoch, logging_interval=10)
test(model, device, test_set_loader)
epoch = 3
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
train(model, device, train_set_loader, optimizer, epoch, logging_interval=10)
test(model, device, test_set_loader)
def test(model, device, test_set_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_set_loader:
data, target = data.to(device), target.to(device)
output = model(data)
# Note: with `reduce=True`, I'm not sure what would happen with a final batch size
# that would be smaller than regular previous batch sizes. For now it works.
test_loss += F.nll_loss(output, target, reduce=True).item() # sum up batch loss
pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_set_loader.dataset)
print("")
print('Test set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)'.format(
test_loss,
correct, len(test_set_loader.dataset),
100. * correct / len(test_set_loader.dataset)))
print("")
def download_mnist(data_path):
if not os.path.exists(data_path):
os.mkdir(data_path)
transformation = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5,), (1.0,))])
training_set = torchvision.datasets.MNIST(data_path, train=True, transform=transformation, download=True)
testing_set = torchvision.datasets.MNIST(data_path, train=False, transform=transformation, download=True)
return training_set, testing_set
batch_size = 1000
DATA_PATH = './data' #set your data path here
training_set, testing_set = download_mnist(DATA_PATH)
train_set_loader = torch.utils.data.DataLoader(
dataset=training_set,
batch_size=batch_size,
shuffle=True)
test_set_loader = torch.utils.data.DataLoader(
dataset=testing_set,
batch_size=batch_size,
shuffle=False)
# Use GPU wherever possible!
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
print(device)
class SpikingNeuronLayer(nn.Module):
def __init__(self, device, n_inputs=28*28, n_hidden=100, decay_multiplier=0.9, threshold=2.0, penalty_threshold=2.5):
super(SpikingNeuronLayer, self).__init__()
self.device = device
self.n_inputs = n_inputs
self.n_hidden = n_hidden
self.decay_multiplier = decay_multiplier
self.threshold = threshold
self.penalty_threshold = penalty_threshold
self.fc = nn.Linear(n_inputs, n_hidden)
self.init_parameters()
self.reset_state()
self.to(self.device)
def init_parameters(self):
for param in self.parameters():
if param.dim() >= 2:
nn.init.xavier_uniform_(param)
def reset_state(self):
self.prev_inner = torch.zeros([self.n_hidden]).to(self.device)
self.prev_outer = torch.zeros([self.n_hidden]).to(self.device)
def forward(self, x):
"""
Call the neuron at every time step.
x: activated_neurons_below
return: a tuple of (state, output) for each time step. Each item in the tuple
are then themselves of shape (batch_size, n_hidden) and are PyTorch objects, such
that the whole returned would be of shape (2, batch_size, n_hidden) if casted.
"""
if self.prev_inner.dim() == 1:
# Adding batch_size dimension directly after doing a `self.reset_state()`:
batch_size = x.shape[0]
self.prev_inner = torch.stack(batch_size * [self.prev_inner])
self.prev_outer = torch.stack(batch_size * [self.prev_outer])
# 1. Weight matrix multiplies the input x
input_excitation = self.fc(x)
# 2. We add the result to a decayed version of the information we already had.
inner_excitation = input_excitation + self.prev_inner * self.decay_multiplier
# 3. We compute the activation of the neuron to find its output value,
# but before the activation, there is also a negative bias that refrain thing from firing too much.
outer_excitation = F.relu(inner_excitation - self.threshold)
# 4. If the neuron fires, the activation of the neuron is subtracted to its inner state
# (and with an extra penalty for increase refractory time),
# because it discharges naturally so it shouldn't fire twice.
do_penalize_gate = (outer_excitation > 0).float()
# TODO: remove following /2?
inner_excitation = inner_excitation - (self.penalty_threshold/self.threshold * inner_excitation) * do_penalize_gate
# 5. The outer excitation has a negative part after the positive part.
outer_excitation = outer_excitation #+ torch.abs(self.prev_outer) * self.decay_multiplier / 2.0
# 6. Setting internal values before returning.
# And the returning value is the one of the previous time step to delay
# activation of 1 time step of "processing" time. For logits, we don't take activation.
delayed_return_state = self.prev_inner
delayed_return_output = self.prev_outer
self.prev_inner = inner_excitation
self.prev_outer = outer_excitation
return delayed_return_state, delayed_return_output
class InputDataToSpikingPerceptronLayer(nn.Module):
def __init__(self, device):
super(InputDataToSpikingPerceptronLayer, self).__init__()
self.device = device
self.reset_state()
self.to(self.device)
def reset_state(self):
# self.prev_state = torch.zeros([self.n_hidden]).to(self.device)
pass
def forward(self, x, is_2D=True):
x = x.view(x.size(0), -1) # Flatten 2D image to 1D for FC
random_activation_perceptron = torch.rand(x.shape).to(self.device)
return random_activation_perceptron * x
class OutputDataToSpikingPerceptronLayer(nn.Module):
def __init__(self, average_output=True):
"""
average_output: might be needed if this is used within a regular neural net as a layer.
Otherwise, sum may be numerically more stable for gradients with setting average_output=False.
"""
super(OutputDataToSpikingPerceptronLayer, self).__init__()
if average_output:
self.reducer = lambda x, dim: x.sum(dim=dim)
else:
self.reducer = lambda x, dim: x.mean(dim=dim)
def forward(self, x):
if type(x) == list:
x = torch.stack(x)
return self.reducer(x, 0)
class SpikingNeuralNetwork(nn.Module):
def __init__(self, device, n_time_steps, begin_eval):
super(SpikingNeuralNetwork, self).__init__()
assert (0 <= begin_eval and begin_eval < n_time_steps)
self.device = device
self.n_time_steps = n_time_steps
self.begin_eval = begin_eval
self.input_conversion = InputDataToSpikingPerceptronLayer(device)
self.layer1 = SpikingNeuronLayer(
device, n_inputs=28*28, n_hidden=100,
decay_multiplier=0.9, threshold=1.0, penalty_threshold=1.5
)
self.layer2 = SpikingNeuronLayer(
device, n_inputs=100, n_hidden=10,
decay_multiplier=0.9, threshold=1.0, penalty_threshold=1.5
)
self.output_conversion = OutputDataToSpikingPerceptronLayer(average_output=False) # Sum on outputs.
self.to(self.device)
def forward_through_time(self, x):
"""
This acts as a layer. Its input is non-time-related, and its output too.
So the time iterations happens inside, and the returned layer is thus
passed through global average pooling on the time axis before the return
such as to be able to mix this pipeline with regular backprop layers such
as the input data and the output data.
"""
self.input_conversion.reset_state()
self.layer1.reset_state()
self.layer2.reset_state()
out = []
all_layer1_states = []
all_layer1_outputs = []
all_layer2_states = []
all_layer2_outputs = []
for _ in range(self.n_time_steps):
xi = self.input_conversion(x)
# For layer 1, we take the regular output.
layer1_state, layer1_output = self.layer1(xi)
# We take inner state of layer 2 because it's pre-activation and thus acts as out logits.
layer2_state, layer2_output = self.layer2(layer1_output)
all_layer1_states.append(layer1_state)
all_layer1_outputs.append(layer1_output)
all_layer2_states.append(layer2_state)
all_layer2_outputs.append(layer2_output)
out.append(layer2_state)
out = self.output_conversion(out[self.begin_eval:])
return out, [[all_layer1_states, all_layer1_outputs], [all_layer2_states, all_layer2_outputs]]
def forward(self, x):
out, _ = self.forward_through_time(x)
return F.log_softmax(out, dim=-1)
def visualize_all_neurons(self, x):
assert x.shape[0] == 1 and len(x.shape) == 4, (
"Pass only 1 example to SpikingNeuralNetwork.visualize(x) with outer dimension shape of 1.")
_, layers_state = self.forward_through_time(x)
for i, (all_layer_states, all_layer_outputs) in enumerate(layers_state):
layer_state = torch.stack(all_layer_states).data.cpu().numpy().squeeze().transpose()
layer_output = torch.stack(all_layer_outputs).data.cpu().numpy().squeeze().transpose()
self.plot_layer(layer_state, title="Inner state values of neurons for layer {}".format(i))
self.plot_layer(layer_output, title="Output spikes (activation) values of neurons for layer {}".format(i))
def visualize_neuron(self, x, layer_idx, neuron_idx):
assert x.shape[0] == 1 and len(x.shape) == 4, (
"Pass only 1 example to SpikingNeuralNetwork.visualize(x) with outer dimension shape of 1.")
_, layers_state = self.forward_through_time(x)
all_layer_states, all_layer_outputs = layers_state[layer_idx]
layer_state = torch.stack(all_layer_states).data.cpu().numpy().squeeze().transpose()
layer_output = torch.stack(all_layer_outputs).data.cpu().numpy().squeeze().transpose()
self.plot_neuron(layer_state[neuron_idx], title="Inner state values neuron {} of layer {}".format(neuron_idx, layer_idx))
self.plot_neuron(layer_output[neuron_idx], title="Output spikes (activation) values of neuron {} of layer {}".format(neuron_idx, layer_idx))
def plot_layer(self, layer_values, title):
"""
plot the layer
"""
width = max(16, layer_values.shape[0] / 8)
height = max(4, layer_values.shape[1] / 8)
plt.figure(figsize=(width, height))
plt.imshow(
layer_values,
interpolation="nearest",
cmap=plt.cm.rainbow
)
plt.title(title)
plt.colorbar()
plt.xlabel("Time")
plt.ylabel("Neurons of layer")
plt.show()
def plot_neuron(self, neuron_through_time, title):
width = max(16, len(neuron_through_time) / 8)
height = 4
plt.figure(figsize=(width, height))
plt.title(title)
plt.plot(neuron_through_time)
plt.xlabel("Time")
plt.ylabel("Neuron's activation")
plt.show()
class NonSpikingNeuralNetwork(nn.Module):
def __init__(self):
super(NonSpikingNeuralNetwork, self).__init__()
self.layer1 = nn.Linear(28*28, 100)
self.layer2 = nn.Linear(100, 10)
def forward(self, x, is_2D=True):
x = x.view(x.size(0), -1) # Flatten 2D image to 1D for FC
x = F.relu(self.layer1(x))
x = self.layer2(x)
return F.log_softmax(x, dim=-1)
'''
Training a Spiking Neural Network (SNN)
'''
spiking_model = SpikingNet(device, n_time_steps=128, begin_eval=0)
train_many_epochs(spiking_model)
'''
Training a Feedforward Neural Network (for comparison) - Non-Spiking Neural Network
It has the same number of layers and neurons, and also uses ReLU activation, but it's not an SNN, this one is a regular one as defined in the code above with the class NonSpikingNeuralNetwork.
'''
non_spiking_model = NonSpikingNeuralNetwork().to(device)
train_many_epochs(non_spiking_model)
'''
Let's see how the neurons spiked
'''
data, target = test_set_loader.__iter__().__next__()
# taking 1st testing example:
x = torch.stack([data[0]])
y = target.data.numpy()[0]
plt.figure(figsize=(12,12))
plt.imshow(x.data.cpu().numpy()[0,0])
plt.title("Input image x of label y={}:".format(y))
plt.show()
# plotting neuron's activations:
spiking_model.visualize_all_neurons(x)
print("A hidden neuron that looks excited:")
spiking_model.visualize_neuron(x, layer_idx=0, neuron_idx=0)
print("The output neuron of the label:")
spiking_model.visualize_neuron(x, layer_idx=1, neuron_idx=y)





