A Python library that allows you to make algebraic operations with 1D and 2D arrays

Clear and complete documentation and tests. This ReadMe doesn't include the full list of functions of the library.

Description

  • Work with vectors and matrixes in an easy way.
  • Sum, Subtract and Multiply between different size matrixes.
  • Get the inverse, transpose, adjugate, cofactor and row reduced matrix in a simple line of code.
  • Get the determinant and the range of a matrix.
  • Little more than 11kb.
  • No dependencies.

Usage

Create and print a Matrix

>>> import matrix

# Create instance
>>> x = Matrix([1, 2, 3])
>>> y = Matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]])

# Print instance
>>> print(x.matrix)
[[1, 2, 3]]
>>> print(y.matrix)
[[1, 0, 0], [0, 1, 0], [0, 0, 1]]

Sum

Now let's sum another matrix to the instance using the sum() method:

>>> y = x.sum([3, 2, 1])
# [1, 2, 3] + [3, 2, 1] = [4, 4, 4]

>>> print(y.matrix)
[[4, 4, 4]]

Subtract

Now let's subtract another matrix to the instance using the minus() method:

>>> y = x.sum([3, 2, 1])
# [1, 2, 3] - [3, 2, 1] = [-2, 0, 2]

>>> print(y.matrix)
[[-2, 0, 2]]

Multiply

Example of how to multiply matrixes using the multiply() method. Remember that some multiply operations between matrixes are incompatible because of their sizes.

>>> x = Matrix([1, 2, 3])
>>> z = x.multiply([[1], [2], [3]])
# [1, 2, 3] * [1] = [14]
#             [2]
#             [3]

>>> print(z.matrix)
[[14]]

Transpose a matrix

Image from Cuemath

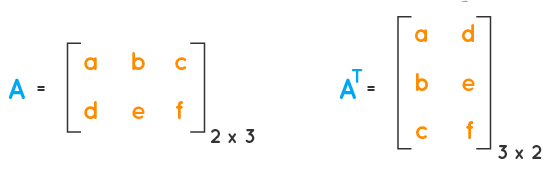
image

Call the transpose() method.

>>> x = Matrix([1, 2, 3])
>>> z = x.transpose()

>>> print(z.matrix)
[[1], [2], [3]]

Inverse of a matrix

Call the inverse() method. Example for regular matrix:

>>> x = Matrix([[1, 2, 3], [3, 2, 1], [1, 0, 3]])
>>> z = x.inverse()

>>> print(z.matrix)
[[-0.375, 0.375, 0.25], [0.5, -0.0, -0.5], [0.125, -0.125, 0.25]]

Example for singular matrix:

>>> x = Matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
>>> z = x.inverse()

>>> print(z.matrix)
[[nan, nan, nan], [nan, nan, nan], [nan, nan, nan]]
# Means that matrix is singular (no inversible)

Cofactor matrix

Call the cofactor() method

>>> x = Matrix([[1, 2, 3], [3, 2, 1], [1, 0, 3]])
>>> z = x.adjugate()

>>> print(z.matrix)
[[6, -8, -2], [-6, 0, 2], [-4, 8, -4]]

Adjugate of a matrix

Call the adjugate() method

>>> x = Matrix([[1, 2, 3], [3, 2, 1], [1, 0, 3]])
>>> z = x.adjugate()

>>> print(z.matrix)
[[6, -6, -4], [-8, 0, 8], [-2, 2, -4]]

Row reduction

From sites.millersville.edu:

Row reduction (or Gaussian elimination) is the process of using row operations to reduce a matrix to row reduced echelon form. This procedure is used to solve systems of linear equations, invert matrices, compute determinants, and do many other things.

Call the row_reduction() method to reduce a matrix:

>>> x = Matrix([[1, 2, 3], [3, 2, 1], [1, 0, 3]])
>>> z = x.row_reduction()

>>> print(z.matrix)
[[1.0, 0.0, 0.0], [-0.0, 1.0, 0.0], [0.0, 0.0, 1.0]]

Can I contribute?

Of course you can! Contributers are necessary for mantaining and improve the library. If you want to contribute, do not hesitate to make a pull request. If you need some information on how to contribute on a Github project, this reading  might be useful.

GitHub - AlexSp3/Matrix.py: A Python library that allows you to make algebraic operations with 1D and 2D arrays
A Python library that allows you to make algebraic operations with 1D and 2D arrays - GitHub - AlexSp3/Matrix.py: A Python library that allows you to make algebraic operations with 1D and 2D arrays
GitHubAlexSp3