torch-householder
This repository implements the Householder transformation algorithm for calculating orthogonal matrices and Stiefel frames. The algorithm is implemented as a Python package with differentiable bindings to PyTorch. In particular, the package provides an enhanced drop-in replacement for the torch.orgqr function.
Overview
APIs for orthogonal transformations have been around since LAPACK; however, their support in the deep learning
frameworks is lacking. Recently, orthogonal constraints have become popular in deep learning as a way to regularize
models and improve training dynamics [1, 2],
and hence the need to backpropagate through orthogonal transformations arised.
PyTorch 1.7 implements matrix exponential function torch.matrix_exp, which can be repurposed to performing the
orthogonal transformation when the input matrix is skew-symmetric. This is the baseline we use in Speed and
Precision evaluation.
Compared to torch.matrix_exp, the Householder transformation implemented in this package has the following advantages:
- Orders of magnitude lower memory footprint
- Ability to transform non-square matrices (Stiefel frames)
- A significant speed-up for non-square matrices
- Better numerical precision for all matrix and batch sizes
Usage
Installation
pip install torch-householder
API
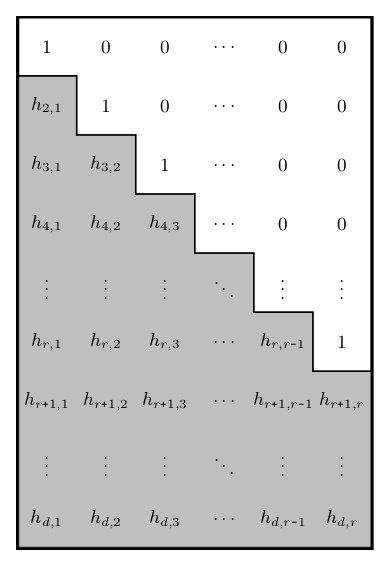
The Householder transformation takes a matrix of Householder reflectors parameters of shape d x r with
d >= r > 0 (denoted as 'thin' matrix from now on) and produces an orthogonal matrix of the same shape.
torch_householder_orgqr(param) is the recommended API in the Deep Learning context. Other arguments of this function
are provided for compatibility with the torch.orgqr
(Reference) interface.
Unlike torch.orgqr, torch_householder_orgqr supports:
- Both CPU and GPU devices
- Backpropagation through arguments
- Batched inputs
The parameter param is a matrix of size d x r or a batch of matrices b x d x r of Householder reflectors
parameters. The LAPACK convention suggests to structure the matrix of parameters as shown in the figure on the right.
Given a matrix param of size d x r, here is a simple way to construct a valid matrix of Householder reflectors
parameters from it:
hh = param.tril(diagonal=-1) + torch.eye(d, r)
This result can be used as an argument to torch_householder_orgqr.
Example
import torch
from torch_householder import torch_householder_orgqr
D, R = 4, 2
param = torch.randn(D, R)
hh = param.tril(diagonal=-1) + torch.eye(D, R)
mat = torch_householder_orgqr(hh)
print(mat) # a 4x2 Stiefel frame
print(mat.T.mm(mat)) # a 2x2 identity matrix
Output:
tensor([[ 0.4141, -0.3049],
[ 0.2262, 0.5306],
[-0.5587, 0.6074],
[ 0.6821, 0.5066]])
tensor([[ 1.0000e+00, -2.9802e-08],
[-2.9802e-08, 1.0000e+00]])
Speed
Given a tuple of b (batch size), d (matrix height), and r (matrix width), we generate a random batch of orthogonal
parameters of the given shape and perform a fixed number of orthogonal transformations with both torch.matrix_exp and
torch_householder_orgqr functions. We then associate each such tuple with a ratio of run times taken by functions.
We perform a sweep of matrix dimensions d and r, starting with 1 and doubling each time until reaching 32768.
The batch dimension is swept similarly until reaching the maximum size of 2048. The sweeps were performed
on a single NVIDIA P-100 GPU with 16 GB of RAM using the code from the benchmark:
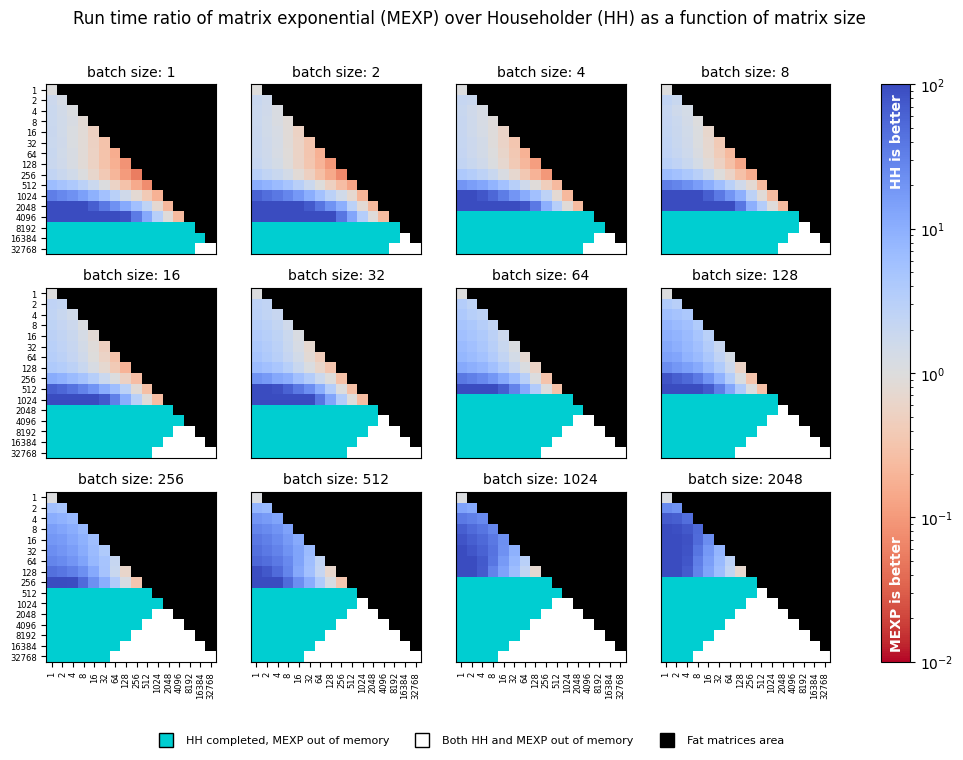
Since the ORGQR function's convention assumes only thin matrices with d >= r > 0, we skip the evaluation of fat
matrices altogether.
The torch.matrix_exp only deals with square matrices; hence to parameterize a thin matrix with d > r, we perform
transformation of a square skew-symmetric matrix d x d and then take a d x r minor from the result. This aspect
makes torch.matrix_exp especially inefficient for parameterizing Stiefel frames and provides major speed gains to the
Householder transformation.
Numerical Precision
The numerical precision of an orthogonal transformation is evaluated using a synthetic test.
Given a matrix size d x r, we generate random inputs and perform orthogonal transformation with the tested function.
Since the output M of size d x r is expected to be a Stiefel frame, we calculate transformation error using the
formula below. This calculation is repeated for each matrix size at least 5 times, and the results are averaged.
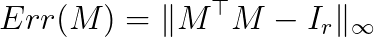
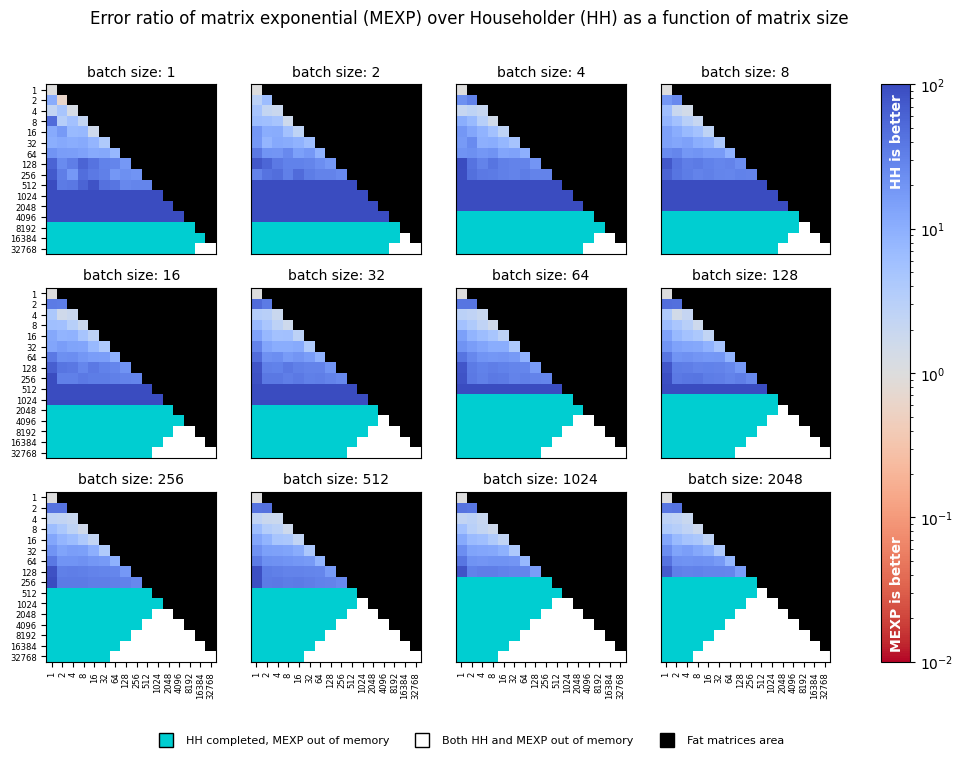
We re-use the sweep used for benchmarking speed, compute errors of both functions using the formula above, and
report their ratio in the following chart:
Conclusions
The speed chart suggests that the Householder transformation is especially efficient when either matrix width
r is smaller than matrix height d or when batch size is comparable with matrix dimensions. In these cases, the
Householder transformation provides up to a few orders of magnitude speed-up. However, for the rest of the square matrix
cases, torch.matrix_exp appears to be faster.
Another benefit of torch_householder_orgqr is its memory usage, which is much lower than that of
torch.matrix_exp. This property allows us to transform either much larger matrices, or larger batches with
torch_householder_orgqr. To give an example, in sub-figure corresponding to "batch size: 1", the largest matrix
transformed with torch_householder_orgqr has the size 16384 x 16384, whereas the largest matrix transformed with
torch.matrix_exp is only 4096 x 4096.
As can be seen from the precision chart, tests with the Householder transformation lead to
orders of magnitude more accurate orthogonality constraints in all tested configurations.
Citation
To cite this repository, use the following BibTeX:
@misc{obukhov2021torchhouseholder,
author = {Anton Obukhov},
year = 2021,
title = {Efficient Householder transformation in PyTorch},
url = {www.github.com/toshas/torch-householder}
}



