Enoki
Enoki is a C++ template library that enables automatic transformations of numerical code, for instance to create a "wide" vectorized variant of an algorithm that runs on the CPU or GPU, or to compute gradients via transparent forward/reverse-mode automatic differentation.
The core parts of the library are implemented as a set of header files with no dependencies other than a sufficiently C++17-capable compiler (GCC >= 8.2, Clang >= 7.0, Visual Studio >= 2017). Enoki code reduces to efficient SIMD instructions available on modern CPUs and GPUs—in particular, Enoki supports:
Deploying a program on top of Enoki usually serves three goals:
-
Enoki ships with a convenient library of special functions and data
structures that facilitate implementation of numerical code (vectors,
matrices, complex numbers, quaternions, etc.). -
Programs built using these can be instantiated as wide versions that
process many arguments at once (either on the CPU or the GPU).Enoki is also structured in the sense that it handles complex programs
with custom data structures, lambda functions, loadable modules, virtual
method calls, and many other modern C++ features. -
If derivatives are desired (e.g. for stochastic gradient descent), Enoki
performs transparent forward or reverse-mode automatic differentiation of
the entire program.
Finally, Enoki can do all of the above simultaneously: if desired, it can
compile the same source code to multiple different implementations (e.g.
scalar, AVX512, and CUDA+autodiff).
Motivation
The development of this library was prompted by the by the author's frustration
with the current vectorization landscape:
-
Auto-vectorization in state-of-the-art compilers is inherently local. A
computation whose call graph spans separate compilation units (e.g. multiple
shared libraries) simply can't be vectorized. -
Data structures must be converted into a Structure of Arrays (SoA) layout
to be eligible for vectorization.
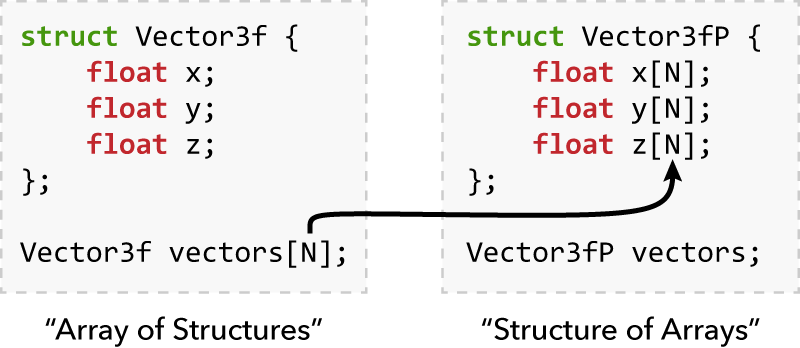
This is analogous to performing a matrix transpose of an application's
entire memory layout—an intrusive change that is likely to touch almost
every line of code.
- Parts of the application likely have to be rewritten using intrinsic
instructions,
which is going to look something like this:
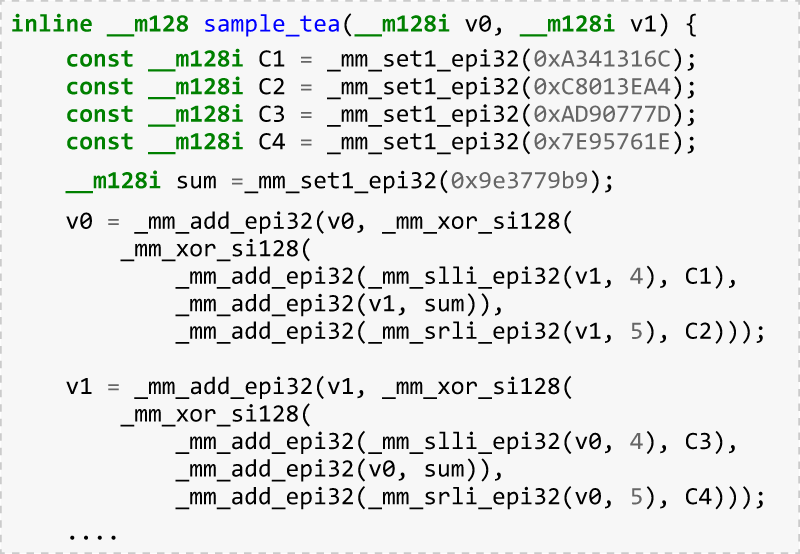
Intrinsics-heavy code is challenging to read and modify once written, and it
is inherently non-portable. CUDA provides a nice language environment
for programming GPUs but does nothing to help with the other requirements
(vectorization on CPUs, automatic differentiation).
-
Vectorized transcendental functions (exp, cos, erf, ..) are not widely
available. Intel, AMD, and CUDA provide proprietary implementations, but many
compilers don't include them by default. -
It is desirable to retain both scalar and vector versions of an algorithm,
but ensuring their consistency throughout the development cycle becomes a
maintenance nightmare. -
Domain-specific languages (DSLs) for vectorization such as
ISPC address many of the above issues but assume
that the main computation underlying an application can be condensed into a
compact kernel that is implementable using the limited language subset of
the DSL (e.g. plain C in the case of ISPC).This is not the case for complex applications, where the "kernel" may be
spread out over many separate modules involving high-level language features
such as functional or object-oriented programming.
What Enoki does differently
Enoki addresses these issues and provides a complete solution for vectorizing
and differentiating modern C++ applications with nontrivial control flow and
data structures, dynamic memory allocation, virtual method calls, and vector
calls across module boundaries. It has the following design goals:
-
Unobtrusive. Only minor modifications are necessary to convert existing
C++ code into its Enoki-vectorized equivalent, which remains readable and
maintainable. -
No code duplication. It is generally desirable to provide both scalar
and vectorized versions of an API, e.g. for debugging, and to preserve
compatibility with legacy code. Enoki code extensively relies on class and
function templates to achieve this goal without any code duplication—the
same code template can be leveraged to create scalar, CPU SIMD, and GPU
implementations, and each variant can provide gradients via automatic
differentiation if desired. -
Custom data structures. Enoki can also vectorize custom data
structures. All the hard work (e.g. conversion to SoA format) is handled by
the C++17 type system. -
Function calls. Vectorized calls to functions in other compilation units
(e.g. a dynamically loaded plugin) are possible. Enoki can even vectorize
method or virtual method calls (e.g.instance->my_function(arg1, arg2, ...);wheninstanceturns out to be an array containing many different
instances). -
Mathematical library. Enoki includes an extensive mathematical support
library with complex numbers, matrices, quaternions, and related operations
(determinants, matrix, inversion, etc.). A set of transcendental and special
functions supports real, complex, and quaternion-valued arguments in single
and double-precision using polynomial or rational polynomial approximations,
generally with an average error of <1/2 ULP on their full domain.
These include exponentials, logarithms, and trigonometric and hyperbolic
functions, as well as their inverses. Enoki also provides real-valued
versions of error function variants, Bessel functions, and elliptical
integrals.
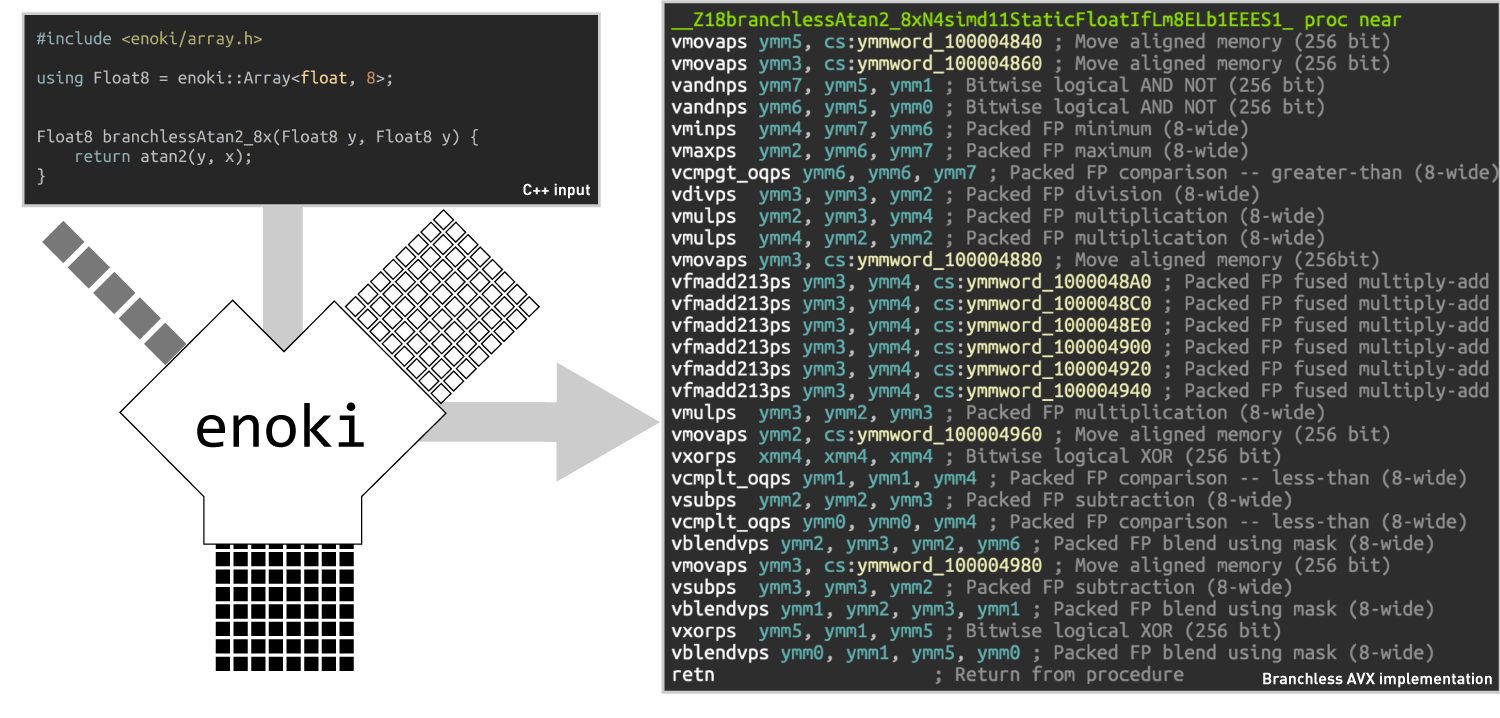
Importantly, all of this functionality is realized using the abstractions of
Enoki, which means that it transparently composes with vectorization,
the JIT compiler for generating CUDA kernels, automatic differentiation, etc.
-
Portability. When creating vectorized CPU code, Enoki supports arbitrary
array sizes that don't necessarily match what is supported by the underlying
hardware (e.g. 16 x single precision on a machine, whose SSE vector only has
hardware support for 4 x single precision operands). The library uses
template metaprogramming techniques to efficiently map array expressions
onto the available hardware resources. This greatly simplifies development
because it's enough to write a single implementation of a numerical
algorithm that can then be deployed on any target architecture. There are
non-vectorized fallbacks for everything, thus programs will run even on
unsupported architectures (albeit without the performance benefits of
vectorization). -
Modular architecture. Enoki is split into two major components: the
front-end provides various high-level array operations, while the back-end
provides the basic ingredients that are needed to realize these operations
using the SIMD instruction set(s) supported by the target architecture.The CPU vector back-ends e.g. make heavy use of SIMD intrinsics to
ensure that compilers generate efficient machine code. The
intrinsics are contained in separate back-end header files (e.g.
array_avx.hfor AVX intrinsics), which provide rudimentary
arithmetic and bit-level operations. Fancier operations (e.g.
atan2) use the back-ends as an abstract interface to the hardware,
which means that it's simple to support other instruction sets such
as a hypothetical future AVX1024 or even an entirely different
architecture (e.g. a DSP chip) by just adding a new back-end. -
License. Enoki is available under a non-viral open source license
(3-clause BSD).
Cloning
Enoki depends on two other repositories
(pybind11 and
cub) that are required when using certain
optional features, specifically differentiable GPU arrays with Python bindings.
To fetch the entire project including these dependencies, clone the project
using the --recursive flag as follows:
$ git clone --recursive https://github.com/mitsuba-renderer/enoki
Documentation
An extensive set of tutorials and reference documentation are available at
readthedocs.org.
About
This project was created by Wenzel Jakob.
It is named after Enokitake, a type
of mushroom with many long and parallel stalks reminiscent of data flow in
vectorized arithmetic.
Enoki is the numerical foundation of version 2 of the Mitsuba
renderer, though it is
significantly more general and should be a trusty tool for a variety of
simulation and optimization problems.
When using Enoki in academic projects, please cite
@misc{Enoki,
author = {Wenzel Jakob},
year = {2019},
note = {https://github.com/mitsuba-renderer/enoki},
title = {Enoki: structured vectorization and differentiation on modern processor architectures}
}



