scikit-fem
scikit-fem is a lightweight Python 3.7+ library for performing finite element assembly. Its main purpose is the transformation of bilinear forms into sparse matrices and linear forms into vectors. The library supports triangular, quadrilateral, tetrahedral and hexahedral meshes as well as one-dimensional problems.
The library fills a gap in the spectrum of finite element codes. The library is lightweight and has minimal dependencies. It contains no compiled code meaning that it's easy to install and use on all platforms that support NumPy. Despite being fully interpreted, the code has a reasonable performance.
Installation
The most recent release can be installed simply by
pip install scikit-fem
or
conda install -c conda-forge scikit-fem
Examples
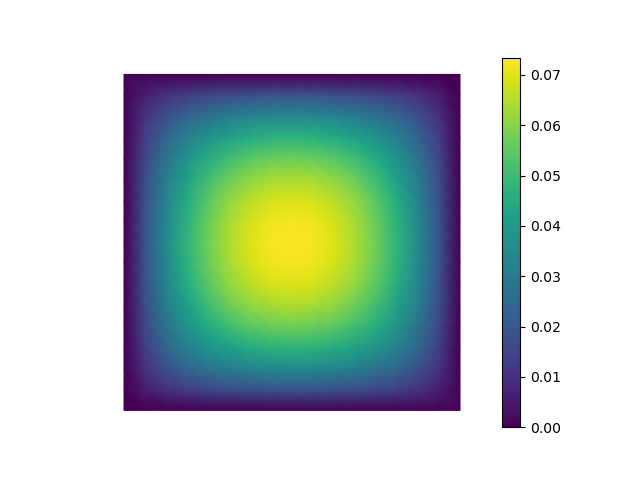
Solve the Poisson problem (see also ex01.py):
from skfem import *
from skfem.helpers import dot, grad
# create the mesh
m = MeshTri().refined(4)
# or, with your own points and cells:
# m = MeshTri(points, cells)
e = ElementTriP1()
basis = InteriorBasis(m, e)
# this method could also be imported from skfem.models.laplace
@BilinearForm
def laplace(u, v, _):
return dot(grad(u), grad(v))
# this method could also be imported from skfem.models.unit_load
@LinearForm
def rhs(v, _):
return 1.0 * v
A = asm(laplace, basis)
b = asm(rhs, basis)
# or:
# A = laplace.assemble(basis)
# b = rhs.assemble(basis)
# enforce Dirichlet boundary conditions
A, b = enforce(A, b, D=m.boundary_nodes())
# solve -- can be anything that takes a sparse matrix and a right-hand side
x = solve(A, b)
# plot the solution
from skfem.visuals.matplotlib import plot, savefig
plot(m, x, shading='gouraud', colorbar=True)
savefig('solution.png')
Meshes can be initialized manually, loaded from external files using
meshio, or created with the help of special
constructors:
import numpy as np
from skfem import MeshLine, MeshTri, MeshTet
mesh = MeshLine(np.array([0., .5, 1.]))
mesh = MeshTri(
np.array([[0., 0.],
[1., 0.],
[0., 1.]]).T,
np.array([[0, 1, 2]]).T,
)
mesh = MeshTri.load("docs/examples/meshes/square.msh")
mesh = MeshTet.init_tensor(*((np.linspace(0, 1, 60),) * 3))
We support many common finite
elements.
Below the stiffness matrix is assembled using second-order tetrahedra:
from skfem import InteriorBasis, ElementTetP2
basis = InteriorBasis(mesh, ElementTetP2()) # quadratic tetrahedron
A = laplace.assemble(basis) # type: scipy.sparse.csr_matrix
More examples can be found in the gallery.
Benchmark
The following benchmark (docs/examples/performance.py) demonstrates the time
spent on finite element assembly in comparison to the time spent on linear
solve. The given numbers were calculated using a ThinkPad X1 Carbon laptop (7th
gen). Note that the timings are only illustrative as they depend on, e.g., the
type of element used, the number of quadrature points used, the type of linear
solver, and the complexity of the forms. This benchmark solves the Laplace
equation using linear tetrahedral elements and the default direct sparse solver
of scipy.sparse.linalg.spsolve.
| Degrees-of-freedom | Assembly (s) | Linear solve (s) |
|---|---|---|
| 4096 | 0.04805 | 0.04241 |
| 8000 | 0.09804 | 0.16269 |
| 15625 | 0.20347 | 0.87741 |
| 32768 | 0.46399 | 5.98163 |
| 64000 | 1.00143 | 36.47855 |
| 125000 | 2.05274 | nan |
| 262144 | 4.48825 | nan |
| 512000 | 8.82814 | nan |
| 1030301 | 18.25461 | nan |