ProbNumDiffEq.jl
ProbNumDiffEq.jl provides probabilistic ODE solvers for the DifferentialEquations.jl ecosystem.
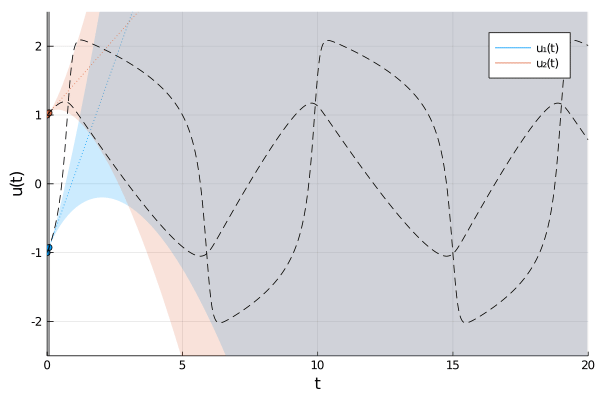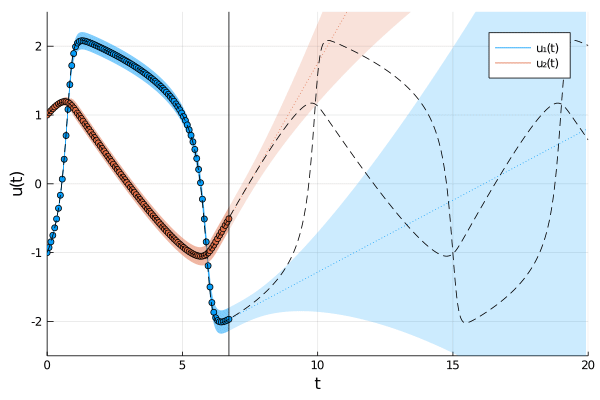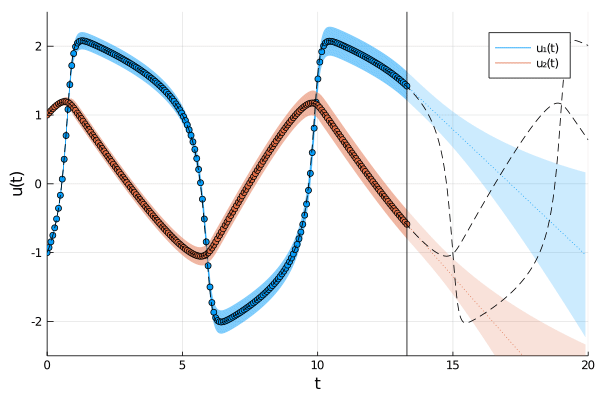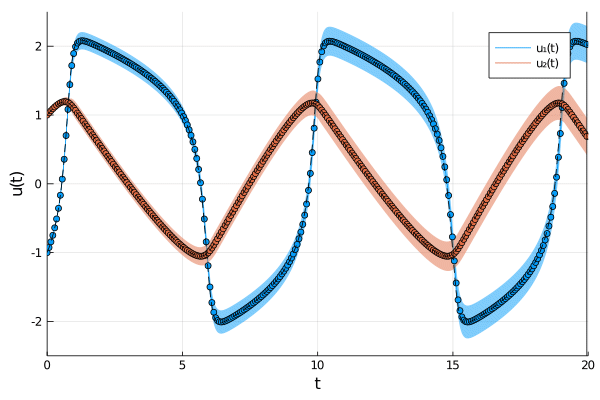
The field of Probabilistic Numerics aims to quantify numerical uncertainty arising from finite computational resources. This package implements ODE filters, a class of probabilistic numerical methods for solving ordinary differential equations. By casting the solution of ODEs as a problem of Bayesian inference, they solve ODEs with methods of Bayesian filtering and smoothing. As a result, the solvers return a posterior probability distribution over ODE solutions and provide estimates of their own numerical approximation error.
Installation
The package can be installed directly with the Julia package manager:
] add ProbNumDiffEq
Example
using ProbNumDiffEq
# ODE definition as in DifferentialEquations.jl
function fitz(u, p, t)
a, b, c = p
return [c*(u[1] - u[1]^3/3 + u[2])
-(1/c)*(u[1] - a - b*u[2])]
end
u0 = [-1.0; 1.0]
tspan = (0., 20.)
p = (0.2,0.2,3.0)
prob = ODEProblem(fitz, u0, tspan, p)
# Solve the ODE with a probabilistic numerical solver: EK0
sol = solve(prob, EK0(), abstol=1e-1, reltol=1e-2)
# Plot the solution
using Plots
plot(sol, fillalpha=0.15)
# Sample from the solution and plot the samples
samples = ProbNumDiffEq.sample(sol, 100)
for i in 1:100
plot!(sol.t, samples[:, :, i], color=[1 2], label="", linewidth=0.1)
end




